En otros términos, las medidas de dispersión en la estadistica descriptiva son números que indican si una variable se mueve mucho, poco, más o menos que otra. El motivo de ser de esta clase de medidas es conocer de forma resumida una característica de la variable estudiada. En este sentido, tienen que escoltar a las medidas de tendencia central. Juntas, ofrecen información de un solamente vistazo que después vamos a poder usar para equiparar y, si fuera preciso, tomar elecciones.
Principales medidas de dispersion
Las medidas de dispersión más conocidas son: el rango, la varianza, la desviación clásica y el coeficiente de alteración (no confundir con coeficiente de determinación). Luego observaremos estas 4 medidas.
Rango
El rango es un costo numérico que sugiere la diferencia entre el costo más alto y el mínimo de una población o muestra estadística. Su fórmula es:
R = Máxx – Mínx
Donde:
- R → Es el rango.
- Máx → Es el costo mayor de la muestra o población.
- Mín → Es el costo mínimo de la muestra o población estadística.
- x → Es la variable sobre la que se pretende calcular esta medida.
Varianza
La varianza es una medida de dispersión que representa la variabilidad de una secuencia de datos en relación a su media. Formalmente se calcula como la suma de los residuos al cuadrado divididos entre el total de visualizaciones. Su fórmula es la siguiente:
- X → Variable sobre la que se pretenden calcular la varianza
- xi → Observación número i de la variable X. i puede tomará valores entre 1 y n.
- N → Número de visualizaciones.
- x̄ → Es la media de la variable X.
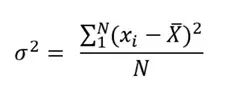
Desviación standard
La desviación clásica es otra medida que da información de la dispersión en relación a la media. Su cálculo es exactamente el mismo que la varianza, empero llevando a cabo la raíz cuadrada de su resultado. O sea, la desviación tradicional es la raíz cuadrada de la varianza.
- X → Variable sobre la que se pretenden calcular la varianza
- xi → Observación número i de la variable X. i puede tomará valores entre 1 y n.
- N → Número de visualizaciones.
- x̄ → Es la media de la variable X.
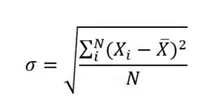
Coeficiente de Variación
Su cálculo se recibe de dividir la desviación tradicional entre el costo absoluto de la media del grupo y en la mayoría de los casos se expresa en porcentaje para su mejor comprensión.
- X → Variable sobre la que se pretenden calcular la varianza
- σx → Desviación clásica de la variable X.
- | x̄ | → Es la media de la variable X en costo absoluto con x̄ ≠ 0
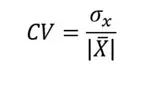
El resumen de las fórmulas presentadas anteriormente son las siguientes:

A efectos comparativos, es fundamental indicar que debemos equiparar constantemente cambiantes con las mismas unidades de medida. Ejemplificando, no tendría mucho sentido mencionar que la variabilidad del producto interior bruto (PIB) es más grande que la de la comercialización de helados. Por poder, se puede indicar, sin embargo equiparar euros con número de helados no posee sentido. Por consiguiente, constantemente mejor equiparar cambiantes con la misma unidad de medida.
Lo mismo pasa con las medidas de dispersión. Si lo cual se desea es equiparar 2 cambiantes, es preferible realizarlo con las mismas medidas de dispersión para todas ellas y de preferencia en la misma unidad.