La estadística descriptiva es una rama de la estadística que se encarga de recopilar, organizar, resumir y presentar datos de una manera que sea comprensible y útil. Su objetivo principal es proporcionar una descripción clara y concisa de conjuntos de datos, lo que ayuda a entender las características fundamentales de los datos y a tomar decisiones informadas basadas en ellos..
Este blog resolvedor de problemas de estadistica descriptiva que comprende diferentes ejercicios. Nos ayuda en nuestra vida diaria, en temas de ingenieria y medicina.
BUSCADOR DE EJERCICIOS DE ESTADISTICA DESCRIPTIVA
Diferencias entre estadística descriptiva e inferencial
La estadística descriptiva y la estadística inferencial son dos ramas de la estadística que tienen propósitos y enfoques diferentes en el análisis de datos. Aquí te presento las principales diferencias entre ambas:
Estadística Descriptiva:
- Objetivo Principal: La estadística descriptiva se centra en describir y resumir datos de manera objetiva. Su objetivo es proporcionar una comprensión clara de un conjunto de datos sin realizar inferencias más allá de esos datos.
- Población de Interés: Se aplica a una población completa o a un conjunto de datos observados. No busca hacer generalizaciones a una población más amplia.
- Medidas Estadísticas: La estadística descriptiva utiliza medidas como la media, la mediana, la moda, la desviación estándar, el rango y las tablas de frecuencia para resumir y visualizar los datos.
- Visualización de Datos: Emplea gráficos y visualizaciones, como histogramas, diagramas de caja y gráficos de barras, para representar la distribución de los datos.
- Muestras: Aunque puede trabajar con datos de muestras, su enfoque principal es describir los datos observados, sin hacer inferencias a partir de esas muestras.
Esta estadistica usa herramientas de matemáticas igualmente que lo hace la física, como de la quimica, la ingeniería o la economía, empero aquello no las hace ser parte de las matemáticas.
Estadística Inferencial:
- Objetivo Principal: La estadística inferencial se utiliza para realizar inferencias, generalizaciones y predicciones basadas en datos muestrales. Su objetivo es sacar conclusiones sobre una población más amplia a partir de una muestra de datos.
- Población de Interés: Se enfoca en hacer generalizaciones a una población más grande utilizando datos de una muestra representativa de esa población.
- Muestras y Parámetros Poblacionales: Utiliza estadísticas muestrales, como medias muestrales y proporciones, para estimar parámetros poblacionales, como la media y la proporción poblacional.
- Pruebas de Hipótesis: La estadística inferencial incluye pruebas de hipótesis que permiten evaluar afirmaciones sobre la población, como si dos grupos son diferentes o si una relación entre variables es significativa.
- Intervalos de Confianza: Calcula intervalos de confianza para estimar la precisión de las estimaciones muestrales de parámetros poblacionales.
- Modelos Estadísticos: Utiliza modelos estadísticos, como regresión y análisis de varianza, para comprender y predecir relaciones y diferencias en los datos.
Esta estadistica tiene relación con los procedimientos usados para lograr hacer predicciones, generalizaciones y obtener conclusiones desde los datos analizados en sus respectivas unidades teniendo presente el nivel de incertidumbre que existe.
En resumen, la estadística descriptiva se enfoca en describir y resumir datos observados sin hacer generalizaciones a una población más amplia, mientras que la estadística inferencial se centra en hacer inferencias basadas en muestras de datos y generalizar esas inferencias a una población más grande. Ambas ramas son fundamentales en la estadística y se utilizan en diferentes contextos según los objetivos de análisis.
Historia de la estadística descriptiva
La historia de la estadística descriptiva se remonta a la antigüedad, pero su desarrollo como disciplina formal se consolidó a lo largo de los siglos XVIII y XIX. Aquí se presenta una breve reseña de su evolución:
- Antigüedad:
- El uso de registros numéricos y censos se puede rastrear hasta las antiguas civilizaciones egipcia y china.
- Los romanos llevaron a cabo censos para diversos propósitos, como la recaudación de impuestos.
- Siglo XVII:
- John Graunt, un mercader londinense, es considerado uno de los pioneros en el uso de datos estadísticos. En su libro «Natural and Political Observations Made upon the Bills of Mortality» (1662), analizó los registros de defunciones en Londres, presentando tablas y análisis sobre tasas de mortalidad.
- Siglo XVIII:
- La obra de Carl Friedrich Gauss, un matemático alemán, contribuyó al desarrollo de la estadística y la teoría de los errores. Gauss introdujo la distribución normal (también conocida como campana de Gauss) y el método de mínimos cuadrados.
- Siglo XIX:
- Sir Francis Galton, primo de Charles Darwin, realizó contribuciones significativas al estudio de la estadística y la correlación. Propuso conceptos como la regresión y la correlación.
- Adolphe Quetelet, un estadístico belga, introdujo conceptos como el índice de masa corporal (IMC) y el «hombre promedio». Sus estudios contribuyeron al desarrollo de la estadística demográfica.
- Siglo XX:
- Durante el siglo XX, la estadística descriptiva se consolidó como una disciplina bien establecida.
- Se desarrollaron técnicas más avanzadas, como el análisis de varianza (ANOVA) y la regresión lineal, que ampliaron la capacidad de describir y analizar datos de manera más precisa.
- La computación moderna permitió un procesamiento de datos más rápido y una visualización más avanzada de los mismos.
- Siglo XXI:
- La estadística descriptiva sigue siendo fundamental en la era de la informática y el análisis de datos masivos (big data).
- Las herramientas de visualización de datos y software estadístico avanzado hacen que la descripción y presentación de datos sean más accesibles y poderosas.
Hoy en día, la estadística descriptiva es una parte esencial de la ciencia de datos y se aplica en una amplia variedad de campos, desde la investigación científica hasta la toma de decisiones en los negocios. Su evolución ha sido constante a lo largo de los siglos, y continúa siendo un elemento clave en el análisis y la interpretación de datos.
Objetivos de la estadística descriptiva
Los objetivos de la estadística descriptiva son los siguientes:
- Resumir Datos: La estadística descriptiva tiene como objetivo principal resumir grandes conjuntos de datos en medidas clave, como la media, la mediana, la moda, la desviación estándar, etc. Esto facilita la comprensión y la interpretación de los datos.
- Descripción de Tendencias Centrales: Ayuda a identificar la tendencia central de los datos, es decir, dónde se agrupan la mayoría de las observaciones. Esto se logra mediante medidas como la media, la mediana y la moda.
- Medir la Dispersión: La estadística descriptiva permite medir cuán dispersos o agrupados están los datos alrededor de la medida de tendencia central, lo que se logra mediante medidas como la desviación estándar y el rango.
- Visualización de Datos: Proporciona herramientas para visualizar los datos, como gráficos, histogramas y diagramas de caja, que ayudan a representar visualmente la distribución y los patrones de los datos.
- Identificación de Valores Atípicos (Outliers): Permite detectar valores atípicos que pueden ser errores en los datos o que pueden tener un impacto significativo en los resultados del análisis.
- Resumen de Datos Categóricos: La estadística descriptiva también se aplica a datos categóricos, donde se utilizan tablas de frecuencia y gráficos de barras para resumir y visualizar la frecuencia de las categorías.
- Comparación de Conjuntos de Datos: Facilita la comparación de diferentes conjuntos de datos utilizando medidas y gráficos descriptivos. Esto es útil para tomar decisiones basadas en diferencias y similitudes entre grupos.
- Identificación de Patrones y Tendencias: Ayuda a identificar patrones y tendencias en los datos, lo que puede ser útil para la toma de decisiones, la predicción y la planificación.
- Comunicación de Resultados: La estadística descriptiva proporciona un medio para comunicar de manera efectiva los resultados a otras personas, ya que simplifica la presentación de información compleja en una forma más fácil de entender.
- Base para la Estadística Inferencial: La estadística descriptiva es la base sobre la cual se construye la estadística inferencial, que se utiliza para hacer inferencias y tomar decisiones basadas en datos.
En resumen, la estadística descriptiva desempeña un papel fundamental en la presentación y comprensión de datos. Sus objetivos son proporcionar una descripción clara y concisa de los datos, identificar patrones y tendencias, y preparar los datos para análisis más avanzados y toma de decisiones.
Ejemplos de Estadistica Descriptiva
Actualmente esta pagina muestra como resolver problemas de estadística descriptiva paso a paso de los siguientes tipos de ejercicios de estadistica resueltos:
- Contribuyentes a la estadistica
- Probabilidad
- Medidas de tendencia
- Medidas de Dispersion
- Datos Estadisticos
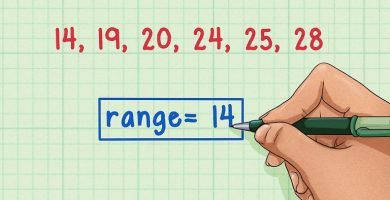
Ventajas y desventajas del rango en estadistica
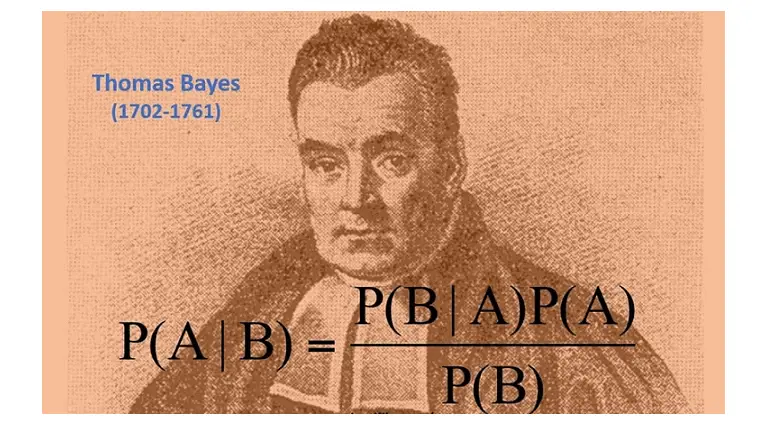
Thomas Bayes

Teorema de chebyshev

Segmentacion de Mercado

Ronald Fisher
Representaciones graficas estadistica
Ejemplos de Estadistica Descriptiva de Medidas de Dispersion
Las medidas de dispersión tratan de lanzar un valor numérico que ofrezca datos sobre el nivel de variabilidad de una variable.
En otros términos, las medidas de dispersión son números que indican si una variable se mueve mucho, poco o más o menos que otra. El motivo de ser de esta clase de medidas es conocer de forma resumida una característica de la variable estudiada.
En este sentido, tienen que escoltar a las medidas de tendencia central. Juntas, ofrecen información de un únicamente vistazo que después vamos a poder usar para equiparar y, si fuera preciso, tomar elecciones.
Ejemplos de Estadistica Descriptiva de Datos Estadisticos
Los tipos de datos estadísticos es la categorización que se hace sobre los datos usados en estadística. Es primordial esta categorización debido a que en funcionalidad del tipo de dato con el que se trabaje, tienen la posibilidad de usar unas técnicas estadísticas u otras.
O sea, los tipos de datos estadísticos son categorías que permiten dividir información con propiedades diferentes. Esta excepción es importante para que los estudiosos sepan cómo hacer la exploración.
Anterior a describir cuáles son los tipos de datos estadísticos que hay, es fundamental tomar en consideración el término de dato. Los datos son la representación de cambiantes estadísticas por medio de la asignación de un costo, letras o símbolos.
Los datos son primordiales para lograr hacer inferencia estadística. La inferencia estadística es el grupo de procedimientos que permiten sustraer conclusiones sobre una población de datos desde una muestra.
Por consiguiente, un dato nos aporta información puntual sobre una variable estadística. Para lograr laborar con ellos, se necesita clasificarlos y ordenarlos de la manera adecuada.
Ejemplos de Estadistica Descriptiva de Contribuyentes a la estadistica
Durante el siglo XIV el concepto «estadística» designaba la recolección sistemática de datos demográficos y económicos por los estados. A comienzos del siglo XIX, el sentido de «estadística» ha sido ampliado para integrar la disciplina ocupada de recolectar, resumir y examinar los datos.
Hoy la estadística es extensamente utilizada en el regimen, los negocios y cada una de las ciencias.
Las pcs electrónicas han acelerado la estadística computacional y permitió a los estadísticos el desarrollo de procedimientos que utilizan recursos informáticos intensivamente.
El concepto «estadística matemática» designa las teorías matemáticas de la posibilidad e inferencia estadística, las cuales son utilizadas en la estadística aplicada. La interacción entre estadística y probabilidades se ha sido desarrollando con la época.
Durante el siglo XIX, las estadísticas utilizaron de manera gradual la teoría de probabilidades, cuyos resultados iniciales fueron encontrados en los siglos XVII y XXI, especialmente en la investigación de los juegos de azar (apuestas).
Para 1600, la astronomía utilizaba modelos probabilísticos y teorías estadísticas. Especialmente el procedimiento de los mínimos cuadrados, el cual ha sido inventado por Legendre y Gauss.
La teoría de las probabilidades y estadísticas ha sido sistematizada y ampliada por Laplace. Luego las probabilidades y estadísticas han experimentado un constante desarrollo.
Durante el siglo XIX el entendimiento estadístico y los modelos probabilísticos fueron utilizados por las ciencias sociales para el progreso. Las novedosas ciencias de psicología empírico, sociología, las ciencias físicas en termodinámica y mecánica estadística.
El desarrollo del argumento estadístico estuvo poderosamente referente con el desarrollo de la lógica inductiva y el procedimiento científico.
Ejemplos de Estadistica Descriptiva de Probabilidad
La posibilidad es un procedimiento por el que se recibe la frecuencia de un evento definido por medio de la ejecución de un experimento aleatorio, del que se conocen todos los resultados probables, bajo condiciones suficientemente estables.
La teoría de la posibilidad se utiliza ampliamente en zonas como la estadística, la física, la matemática, las ciencias y la filosofía para sacar conclusiones sobre la posibilidad discreta de sucesos potenciales y la mecánica subyacente discreta de sistemas complicados, por consiguiente es la rama de las matemáticas que estudia, mide o establece a los experimentos o fenómenos aleatorios.
Ejemplos de Estadistica Descriptiva de Medidas de tendencia
Las medidas de tendencia central son medidas estadísticas que pretenden resumir en un solo valor a un grupo de valores. Representan un centro alrededor del cual está localizado el grupo de los datos. Las medidas de tendencia central más usadas son: media, mediana y moda.
Las medidas de dispersión sin embargo miden el nivel de dispersión de los valores de la variable. Dicho esto es las medidas de dispersión pretenden evaluar en qué medida los datos difieren entre sí.
Los tipos de medidas utilizadas en general permiten explicar un grupo de datos entregando datos acerca de su postura y dispersión.
Los métodos para obtener las medidas estadísticas difieren levemente de la manera en que estén los datos.
Si los datos se hallan ordenados en una tabla estadística mencionaremos que se hallan “agrupados” y si los datos no permanecen en una tabla hablaremos de datos “no agrupados”.
Según este criterio haremos primero el análisis de las medidas estadísticas para datos no agrupados y después para datos agrupados.
