
En las secciones primeras hemos estudiado medidas de tendencia central (media, moda y mediana), y medidas de dispersión (varianza y desviación estándar). Ahora estudiaremos el teorema de chebyshev. También estudiamos el grado de asimetría (sesgo) de una distribución y su curtosis (altura). Es decir, ya logramos describir, en términos generales, el proceder de un conjunto de valores.
Retomando la noción de desviación estándar, expresaremos que una de las aplicaciones que tiene es que logramos utilizarlo para conocer aproximadamente cuántas de las calificaciones se agrupan en ciertos intervalos de la serie hechos por la suma y la resta de una, dos o tres veces el valor de la desviación estándar con relación al valor medio. Para esto es que aprenderemos el Teorema de Tchebyshev.
P. L. T chebyshev (1821- 1894)
Inspeccionó por separado la propiedad de la variabilidad de los datos en torno a la media. Halló que sin interesar cómo se distribuye un conjunto de datos, el porcentaje de observaciones que están comprendidas dentro de distancias de ±k desviaciones estándar junto de la media, se encuentra definido. En las secciones primeras hemos estudiado medidas de tendencia central (media, moda y mediana), y medidas de dispersión (varianza y desviación estándar). Ahora estudiaremos el teorema de chebyshev por la siguiente fórmula:
Para concebir mejor el resultado del teorema advirtamos algunos valores que se logran aplicando la fórmula: Para k = 2, el teorema nos dice que:
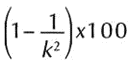
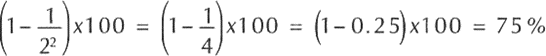
Cuando menos 75% de las observaciones caen en ±2 desviaciones estándar con relación a la media y también se logra expresar manejando un intervalo definido como (x-2s) a (x+2s). Cuando menos 88.89% de las observaciones entre la media +/- 3 desviaciones estándar y al menos 93.75% de los valores se hallarán entre la media y ±4 desviaciones estándar.
No obstante el Teorema de Tchebyshev se puede aplicar a cualquier clase de distribución de valores, si los datos fueran simétricos y acampanados. Exactamente 68.26% de todas las reflexiones estarían comprendidas dentro de distancias de ±1 desviación estándar cerca de la media, mientras que 95.44, 99.73 y 99.99% de las observaciones estarían incluidas dentro de distancias de ±2, ±3, ±4 desviaciones estándar cerca de la media. Se ve en las secciones primeras hemos estudiado moderadas de tendencia central (media, moda y mediana) y medidas de dispersión (varianza y desviación estándar). Ahora estudiaremos el teorema de chebyshev de la consiguiente forma:
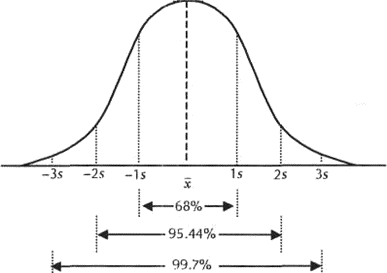
Los efectos del porcentaje de puntuaciones que se reúnen en torno a la media, para cualquier tipo de distribución de tipo normal. Lo logramos resumir en la siguiente tabla:
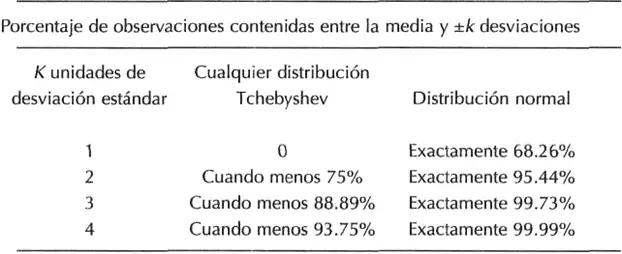
Ejemplo Teorema de chebyshev: Retomando el ejemplo de las edades de 30 personas empañadas al azar en el cual se obtuvo la sucesiva distribución de frecuencias:

- Evidencie que dentro del intervalo de ±2 desviaciones estándar se halla cuando menos 75% de las observaciones de la muestra.
Respuesta Teorema de chebyshev:
Para emplear la fórmula del Teorema de Tchebyshev precisamos primero calcular la media y la desviación estándar de los valores. Pero como ya anticipadamente los teníamos calculado, sólo los retomaremos:
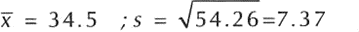
Ahora, empleando la fórmula para k- 2 desviaciones estándar, el teorema testifica que:
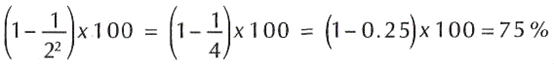
Lo que muestra que cuando menos 75% de las observaciones bajan en el intervalo.
Evidenciemos que esto se cumple. Ejecutando las operaciones tenemos:
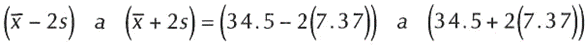
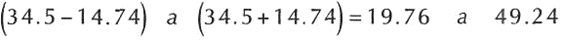
Interpretación Teorema de chebyshev:
Presentando los valores derivados en términos redondeados logramos decir que el intervalo formado por ±2 desviaciones estándar con relación a la media contiene edades de 20 a 49 años. Ahora bien, cuántas puntuaciones de nuestra serie se hallan dentro de ese intervalo. Si estar a la mira nuestra tabla de distribución de frecuencias logramos ver que las edades varían de los 1§ a los 44 años. En este caso de los 20 a los 49 años se encuentran 29 de las 30 observaciones, es decir, (29/30) x 100 – 96.66%, de las observaciones que se hallan contenidas en el intervalo obtenido empleando la fórmula de Tchebyshev.
Definitivamente logramos concluir que, efectivamente, se halla cuando menos 75% de las observaciones contenidas interiormente del intervalo.
