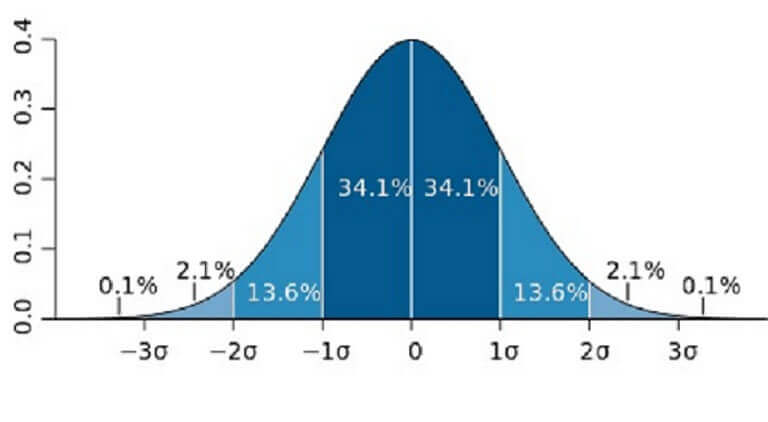
En una distribución de frecuencias la dispersión o variabilidad sugiere hasta que punto es homogénea la desviación estandar y varianza. Así, una vez que los valores de la variable difieren poco entre sí, el nivel de homogeneidad es alto y las medidas de postura central (media) representan el orden de intensidad de los valores de la variable.
En otro caso, una vez que entre los valores de la variable hay enormes diferencias, el reparto es heterogénea, por lo que las medidas de postura central (media) tienen la posibilidad de ser poco representativas. Para que vayamos a comprender la desviacion standard, debemos entender la relación que existe con la varianza y el coeficiente de variación.
VARIANZA, S2
En relación a la media aritmética, es una medida de dispersión. Se puede definir como el promedio de las desviaciones altas elevadas al cuadrado, de los valores considerados en relación a la media.
Se puede simplificar su cálculo usando la siguiente expresión:
La varianza tiene las siguientes propiedades:
Propiedades:
- La varianza constantemente toma valores no negativos.
- Si todos los valores del reparto son equivalentes, la varianza es 0.
- La varianza no cambia una vez que se suma una misma porción a todos los valores vigilados, o sea, una vez que se hace un cambio de procedencia.
- La varianza cambia si se multiplican todas las visualizaciones del reparto por la misma constante, lo que significa una vez que se hace un cambio de escala o cambio de unidades de medida.
- Casi siempre, si a cada una de las visualizaciones de la variable X se aplica un cambio del tipo X’=a+bX, la varianza de la variable transformada S^2 se puede calcular en funcion a la varianza de X, siendo
La varianza tiene los siguientes inconvenientes:
Inconvenientes:
- No muestra la misma unidad de medida que la variable.
- De los cambios de la unidad de medida es dependiente .
- No está acotada.
Desviación estandar
Se define como la raíz^2 positiva de la varianza.
Que la variable y que la media aritmética muestra la misma unidad de medida.
Posibilita implantar intervalos centrados en la media que tienen por lo menos dentro un definido % de visualizaciones. Ejemplificando, el siguiente intervalo cerca de la media tiene como mínimo el 89% de las visualizaciones. Por consiguiente, básicamente tiene todos los valores del reparto y solamente ciertos valores extremos superarán dichos parámetros. O sea, los valores de la variable solamente en algunas ocasiones extremos diferirán de la media.
Caracteristicas desviación estandar
La desviación estandar al igual que la varianza tiene las mismas características: es no negativa, únicamente le están afectando los cambios de escala y es cero una vez que el reparto es constante.
COEFICIENTE DE VARIACION, CV(x)
Es la división de la desviación estandar con el valor absoluto de la media.
Expresa la desviación estandar como % de la media.
El coeficiente de variación es:
Propiedades:
- Es una medida de dispersión relativa (no muestra unidades de medida).
- Cerca de la media de 2 o más distribuciones posibilita equiparar la dispersión aun cuando presenten diversas unidades de medida o medias aritméticas diferentes.
- Los cambios de unidades no le afectan (cambios de escala).
