¿Qué es una prueba t student?
Una prueba t acreditada como prueba t de Student es un instrumento para valorar las medias de uno o dos grupos a través de pruebas de hipótesis. Una prueba t puede utilizar para establecer si un único grupo aplaza de un valor acreditado (una prueba t de una muestra), si dos grupos aplazan entre sí (prueba t de muestras independientes), o si hay una diferencia reveladora en medidas pareadas (una prueba t de muestras dependientes o pareada).
¿Cómo se usan las pruebas t student?
Primero precise la hipótesis que quiera evidenciar y establezca un riesgo asumible de llegar a terminaciones erróneas. Por ejemplo, al cotejar dos grupos, podría estimar que sus medias las mismas y establecer una probabilidad aceptable de ultimar que tuviera una discrepancia cuando no es el caso. A continuación, calcule la estadística de la prueba de sus datos y cotéjala con un dato teórico de la distribución t. En función del consecuencia, o bien rechaza o bien no logra rechazar su hipótesis nula.
Más de dos grupos
No puede utilizar una prueba t. Utilice un método de comparación múltiple. Cualesquiera ejemplos existirían el análisis de varianza ANOVA, la cotejo por pares de Tukey-Kramer, la comparación con control de Dunnett y el análisis de medias ANOM.
No obstante las pruebas t student resisten comparativamente bien las desviaciones de la hipótesis, al hacer una prueba t se asume que:
- Los datos son incesantes.
- La muestra de datos se ha empañado aleatoriamente de la población.
- Hay homogeneidad en la varianza (datos del grupo es similar).
- La distribución es aproximadamente normal.
Para pruebas t de dos muestras, correspondemos tener muestras independientes. Si las muestras no son independientes, logra ser más conveniente una prueba t pareada.
Tipos de prueba t student
Hay tres pruebas t para cotejar medias: la prueba t student de una muestra, la prueba t de dos muestras y la prueba t pareada. La sucesiva tabla resume las tipos de cada una y brinda orientación a la hora de elegir la más conveniente. Visite las páginas determinadas de cada tipo de prueba t para ver ejemplos, conjuntamente de más pormenores.
Prueba t de una muestra
- Sinónimos: Prueba t de Student
- Variables: Uno
- Tipo de variable: Medida continua
- Objetivo de la prueba: Determinar si la media de población es igual o no que un valor específico
- Estimación de la media de población: Media de la muestra
- Desviación estándar de la población: Desconocida
- Grados de libertad: n–1
Prueba t de dos muestras
- Sinónimos: Prueba t combinada
- Variables: Dos
- Tipo de variable: Medida continua
- Categórico o nominal: para definir grupos
- Objetivo de la prueba: Determinar si las medias de población de dos grupos distintos son o no iguales
- Estimación de la media de población: Media de la muestra de cada grupo
- Desviación estándar de la población: Desconocida
- Grados de libertad: n1 + n2 – 2
Prueba t pareada
- Sinónimos: Prueba t de grupos pareados
- Variables: Dos
- Tipo de variable: Medida continua
- Categórico: nominal para definir pares en un grupo
- Objetivo de la prueba: Determinar si la diferencia entre medidas pareadas es o no igual a cero
- Estimación de la media: Media de las diferencias entre pares de la muestra
- Desviación estándar: Desconocida
- Grados de libertad: n–1
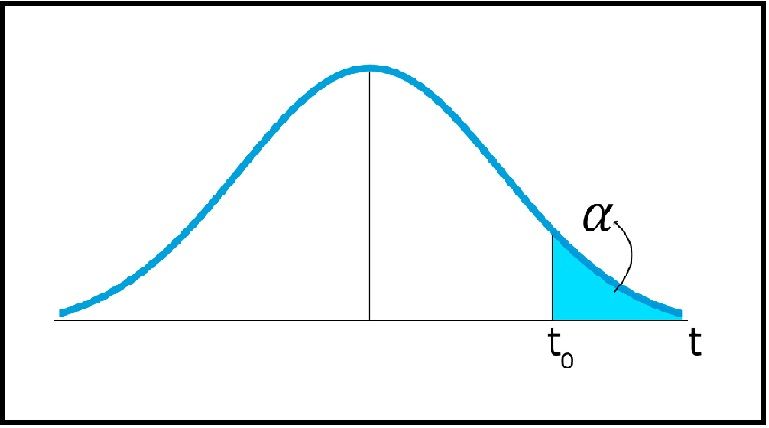
Pruebas unilaterales frente a bilaterales
Si se instituye la hipótesis, asimismo instituye si su prueba es unilateral o bilateral. Puede tomar esta decisión precedentemente de reunir los datos o de principiar cualquier cálculo. Esta fallo se toma en las 3 pruebas t sobre medias.
Para exponer, usemos un ejemplo de prueba t. Conjeturemos que poseemos una muestra aleatoria de barritas de proteínas, y la etiqueta de las mismas indica 90 gr de proteína en cada barrita. La hipótesis nula es que la media poblacional desconocida es 90. Conjeturemos que solo pretendemos saber si los datos muestran que poseemos una media poblacional diferente. En este caso, nuestras hipótesis son:
Ho:μ=90Ho:μ=90
Ha:μ≠90Ha:μ≠90
Aquí tenemos una prueba bilateral. Usaremos los datos para determinar si la media de la muestra es lo bastante distinta de 90, por encima o por debajo, como para declarar que la media poblacional desconocida es distinta de 90.
Supongamos que queremos saber si lo que pone en la etiqueta es correcto. ¿Los datos apoyan la idea de que la media poblacional desconocida es de al menos 90? ¿O no? En este caso, nuestras hipótesis son:
Ho:μ>=90Ho:μ>=90
Ha:μ<90Ha:90<20
Aquí poseemos una prueba unilateral. Utilizaremos los datos para establecer si la media de la muestra es lo suficiente inferior a 90 como para rechazar la hipótesis de que la media poblacional desconocida es igual o mayor a 90.
Examine la sección de «Colas para pruebas de hipótesis» en la hoja sobre distribución t para ver imágenes que instruyen los nociones de pruebas unilaterales y bilaterales.
Cómo realizar una prueba t student
Para todas las pruebas t que implican medias, el análisis conlleva los siguientes pasos:
- Precise su hipótesis nula (Ho) y alternativa (Ha) precedentemente de reunir los datos.
- Resuelva el valor alfa (o valor ?). Esto envuelve establecer el riesgo que desea correr de alcanzar a una conclusión errónea. Por ejemplo, expresemos que define ?=0,05 al cotejar dos grupos independientes. En este caso resuelve correr un riesgo del 5 % de ultimar que las medias poblacionales ignoradas son distintas cuando no lo son.
- Examine probables errores de datos.
- Examine las elevaciones de la prueba.
- Cree la prueba y saque sus conclusiones. Unas las pruebas t de medias envuelven calcular la estadística de la prueba. A continuidad, compare la estadística de la prueba con el valor teórico de la distribución t. El valor teórico envuelve tanto al valor alfa como a los grados de libertad de sus datos. Para más identificaciones, visite las páginas de la prueba t de una modelo, la prueba t de dos muestras y la prueba t pareada.
