
Vale la pena recordar que se llama desviación estándar o desvío a la diferencia entre un valor individual x¡ y la media x . La varianza es una medida de dispersión en la que hallamos las desviaciones al cuadrado. Esto indica que la unidad de varianza se expresa en unidades al cuadrado.
Para superar esta insuficiencia y disponer de una medida de la dispersión de las puntuaciones que se exprese en unidades, que no sean al cuadrado, se calcula la raíz cuadrada de la varianza conocida como desviación estándar.
La desviación estándar es una de las medidas de resumen que más se utiliza para distribuciones y desempeña un papel preponderante en la estadística. Es importante observar que las unidades en las que se expresa la desviación estándar son las mismas que las de la media. Por ejemplo, si la media se da a conocer en unidades monetarias, la desviación estándar también lo estará. Si la media está en metros, lo mismo ocurrirá con la desviación estándar.
Definición: la desviación estándar a, para la población o s, para la muestra, es la desviación en promedio de las diferencias de los valores con respecto a su media.
La desviación estándar es simplemente la raíz cuadrada de la varianza. De este modo, si la varianza es 81. la desviación estándar es 9.

Entonces se deduce que para obtener la desviación se debe calcular la varianza primero y después hallar su raíz cuadrada.
Las fórmulas son las mismas que se utilizaron para la varianza, sólo que ahora se agrega el símbolo de raíz cuadrada en cada una:
Tenemos que recordar que existían dos métodos para calcular la varianza, el primero de ellos:

Para el segundo método las fórmulas son:

Podemos realizar un ejemplo utilizando la segunda fórmula para una serie simple: calcule para esta muestra: 20, 5, 10, 15,25.
| Respuesta: |
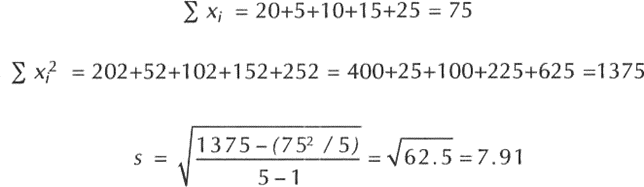
Ejercicio (2.4.4): calcular la desviación estándar de los tres ejemplos anteriores para los cuales se calculó la varianza. Y lo mismo para los ejercicios de 80 y 40 datos con su respectiva interpretación.
Coeficiente de variación (dispersión absoluta y relativa): El coeficiente de variación de una distribución lo podemos definir como la expresión porcentual que representa la desviacion estandar de una muestra con respecto a su media.
En algunos casos las dispersiones, en términos absolutos, pueden ser diferentes a la realidad y por ello se tienen que analizar en términos de coeficientes de variación.
El coeficiente de variación está definido por la siguiente fórmula:
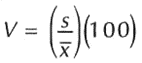
Donde: s es la desviación estandar y x es la media.
Veamos un ejemplo: un fabricante de focos produce dos tipos de foco

son de sA – 280 horas y sB – 310 horas. ¿Qué tipo de foco tiene la mayor
- dispersión absoluta, b) dispersión relativa?
Respuesta:
- Dispersión absoluta de A = sA – 280 horas; de B = sB = 310 horas, entonces B tiene la dispersión absoluta mayor.
- Coeficiente de variación:
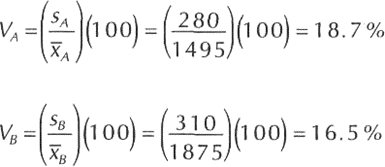
Entonces el tipo de foco A es el que tiene una mayor variación o dispersión relativa.
Ejemplo: considere que un grupo de estudiantes realiza dos pruebas. La primera resulta con una media de 60 puntos y una s = 6 puntos y un máximo de 100 puntos. La segunda tiene una media de 700 puntos y una s-7, con un máximo de 1000 puntos.
a. ¿Cuál de las dos pruebas tiene una variación o dispersión mayor?
Respuesta:
Primera prueba: Segunda prueba:
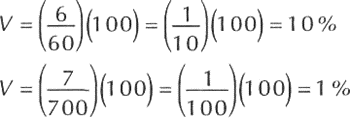
Como se puede ver, la dispersión relativa de la segunda prueba es 1/10, de la primera.
