La probabilidad determina cuantitativamente la posibilidad de que un hecho suceda con un resultado establecido. La posibilidad de que ocurran sucesos aleatorios es medida por la probabilidad.
La asignación de la probabilidad a los diversos sucesos aleatorios se establece implementando alguno de los próximos criterios: Regla de Laplace, que pide equiprobabilidad de los resultados primordiales, la teoría frecuencialista que es de repetición del experimento y una vez que no se otorgan los requisitos anteriores la teoría subjetivista.
La información adicional de la ocurrencia de un evento nos lleva al criterio de posibilidad condicionada y al teorema de la intersección.
Se concluye que dos sucesos son independientes, si la probabilidad de un evento no se ve modificada por otro evento.
El teorema de Bayes vincula la posibilidad de A dado B con la posibilidad de B dado A. Desde una información adicional, posibilita reasignar probabilidades establecidas a priori .
EXPERIMENTO ALEATORIO.
Los fenómenos que están sujetos a azar estudia la estadística como ciencia experimental. Dichos fenómenos aleatorios permanecen asociados a experimentos que tienen la posibilidad de repetir de manera sin límite y muestran resultados indescifrables aun cuando se realicen en las mismas condiciones. Pese a determinados resultados inesperados los experimentos aleatorios, se caracterizan ya que muestran una pauta de comportamiento o regularidad estadística en el tiempo. A continuación se pueden ver los principales conceptos relacionados con experimento aleatorio:
Espacio muestral
El grupo de todos los resultados probables de un experimento aleatorio se denomina espacio muestal.
Suceso aleatorio
Dado un lugar referencial, se define como evento aleatorio de cualquier subconjunto en un espacio referencial. El evento que tiene un solo resultado de E se denomina evento elemental o componente muestral.
Ejemplo. Una caja tiene 1 bola blanca (B), 1 bola negra (N) y 1 bola roja (R). El ensayo esta en sustraer 2 bolas con devolución y mirar la sucesión de colores obtenidos. El espacio muestral o referencial es:
E = {BB,BR,BN,RB,RR,RN,NB,NR,NN}
Sobre este espacio pueden definirse lo siguiente:
A1=Dos bolas del mismo color={BB, RR, NN}
A2=Dos bolas de distinto color={BR,BN,RB,RN,NB,NR}
A3=Por lo menos una bola blanca={BB,BR,BN,RB,NB}
A4=Exactamente una bola blanca={BR,BN, RB,NB}
A5=Ninguna bola blanca={RR,RN,NR,NN}
A6=Dos bolas blancas={BB}
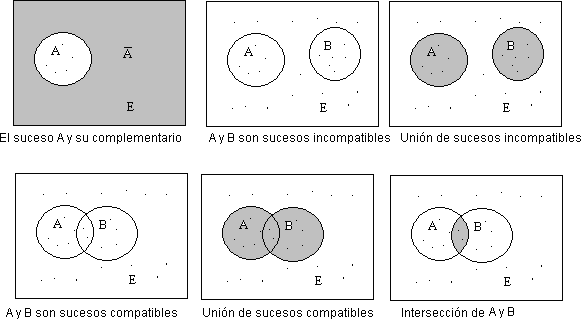
Relaciones entre sucesos aleatorios
Suceso complementario: Dado un suceso A, el suceso complementario que es aquel que contiene todos los resultados del experimento que no están contenidos en A.
Ejemplo 1: ¿Cuál es el suceso complementario a A1={BB,RR,NN} en el siguiente espacio muestral E = {BB,BR,BN,RB,RR,RN,NB,NR,NN}?
De acuerdo a la definición el complementario será {BR,BN,RB,RN,NB,NR}
Suceso unión: Dados Ai y Aj el suceso unión (Ai Aj) es aquel que contiene todos los resultados que pertenecen a Ai y Aj o a ambos.
Ejemplo 2: Si A1={BB, RR, NN} y A3={BB,BR,BN,RB,NB}, cual es el resultado de (A1 U A3 )
De acuerdo a la definición del suceso unión donde se obtienen todos o valores de ambos sucesos el resultado será:
(A1 U A3 )={BB,BR,BN,RB,RR,NB,NN}
(Ai U Aj ) = Los resultados que pertenecen a Aj también pertenecen a Ai de forma que si ocurre Aj ocurre también Ai.
Suceso intersección: El suceso intersección (Ai ∩Aj) es aquel que contiene todos los resultados que pertenecen a Ai y a Aj al mismo tiempo.
Ejemplo 3: Si A1={BB, RR, NN} y A3={BB,BR,BN,RB,NB}, cual es el resultado de (A1 ∩ A3 )
De acuerdo a la definición del suceso unión donde se obtienen todos o valores de ambos sucesos el resultado será:
(A1 ∩ A3)={BB}
Cuando dos sucesos Ai y Aj son tales que (Ai ∩ Aj) = Θ se dice que Ai y Aj son sucesos incompatibles o mutuamente excluyentes.
Debemos conocer lo siguiente de los sucesos intersección:
- La intersección de un suceso A y su complementario es igual al conjunto vacío, por tanto A y su complementario son sucesos incompatibles.
- La intersección puede generalizarse una cantidad mayor de dos sucesos.
PROBABILIDAD. AXIOMÁTICA Y PROPIEDADES