En artículos anteriores hemos abordado cómo examinar en forma crítica la validez de un análisis de terapia y cómo manifestar los resultados con diversas medidas de impacto (riesgo absoluto, peligro relativo, número primordial para tratar).
De esta forma, al instante de ejercer los resultados de un análisis, lo hacemos usando el número que se nos entrega, lo cual conocemos como estimador puntual. Si el análisis se volviera a hacer en condiciones idénticas, empero con una totalmente nueva muestra, es factible que el resultado no sea exactamente igual, debido a que el resultado es una aproximación del resultado real.
El resultado real es el que se obtendría al utilizar la mediación a la población completa, entendiendo población como el total de la poblacional general.
Utilizando los datos tenemos la probabilidad de estimar un rango en el cual está con alta probabilidad el resultado real y es claramente este rango lo cual conocemos como intervalo de confianza.
Este artículo busca contribuir a comprender e interpretar un intervalo de confianza, su interacción con la magnitud muestral y advertir las diferencias comparativas con el resultado P.
Intervalo de confianza: Definición y características
El intervalo de confianza explica la variabilidad entre el tamaño obtenido en un análisis y el tamaño real poblacional. Es de un rango de valores, cuya repartición es usual y en el que está con alta probabilidad el resultado real de una cierta variable. Se ha predeterminado por acuerdo en 95% esta alta probabilidad. Así, un intervalo de confianza de 95% nos sugiere que dentro del rango dado está el resultado real de un parámetro con 95% de certeza.
Supongamos que poseemos una moneda, para entender y hacer intuitivo el término de intervalo de confianza, la cual puede o no estar equilibrada. De esta forma, luego de diversos lanzamientos, la posibilidad que el resultado sea sello variará a partir de 0 (todas las veces cara, o sea, una moneda balanceada) hasta 1 (todas las veces sello, de nuevo balanceada), pasando por 0,5 (la mitad de las veces sello y las demás cara, lo cual equivale a una moneda no balanceada). Vamos a experimentar con ella, como no conocemos la verdadera naturaleza de la moneda.
Experimento lanzando una moneda
Iniciamos el experimento con 2 lanzamientos, uno es cara y el otro sello o sol como se conoce en otros países. La probabilidad de que el resultado sea sello ha sido 0,5, con lo cual podríamos concluir que la moneda no está equilibrada, no obstante, ¿con solamente 2 lanzamientos tenemos la probabilidad de concluir la naturaleza de la moneda?
Ya que el azar ha podido influir en este resultado, uno acepta que el rango de valores reales probables es extenso, inclusive a partir de uno tan bajo como 0 a uno tan elevado como 1, por consiguiente todavía no estamos seguros de la naturaleza de nuestra moneda.
Viendo lo anterior, ampliamos el experimento y realizamos 8 nuevos lanzamientos (10 total), resultando 5 caras y 5 sellos. De nuevo el resultado es 0,5, no obstante, ahora intuitivamente nos damos cuenta que la verdadera naturaleza de la moneda está en un rango menos extenso. Ejemplo: Es poco viable que luego de 10 lanzamientos 9 sean sello, menos todavía que todos lo sean, no obstante, todavía es probable que 8 ó 7 ó 6 sí lo sean.
Asi, el nuevo rango puede variar entre 0,2 y 0,8, sin embargo con un alcance todos advertimos que si bien 0,8 y 0,2 son probables, los valores centrales (0,4 y 0,6) lo son más todavía, siendo 0,5 el más probable.
Decidimos continuar experimentando, llevando a cabo 90 nuevos lanzamientos (100 en total), resultando 50 caras y 50 sellos. De nuevo el resultado es 0,5, advirtiendo que cada vez es más probable que la verdadera naturaleza de la moneda es el de una no equilibrada, empero todavía con un rango de variabilidad que se podría estimar que esta entre 0,4 y 0,6.
Realizamos 1.000 lanzamientos, resultando 500 sellos y 500 caras, con lo cual estamos todavía más seguros que nuestra moneda no está equilibrada.
Conceptos a tomar en cuenta
El ejemplo anterior posibilita tener en claro lo siguiente:
- Corresponde al resultado real, la verdadera naturaleza de nuestra moneda (si está equilibrada o no).
- Corresponde al intervalo de confianza, el rango de valores reales probables, o sea el rango donde está la verdadera naturaleza de nuestra moneda.
- El resultado real más posible corresponde al estimador puntual del análisis, en esta situación 0,5.
- Al final, advertimos la interacción inversa entre la amplitud del intervalo de confianza y la magnitud muestral: si consideramos que el número de lanzamientos representa el n de la muestra, se vee que a medida que más pequeño es n más extenso es el intervalo de confianza. A más grande número de lanzamientos (mayor n) más certeza poseemos que el resultado del experimento se acerca al resultado real, por consiguiente el intervalo de confianza es más estrecho.
Para llevar a la práctica vamos a recurrir a un ejemplo: la comparación de una nueva droga A versus una droga B en la prevención de trastornos psiquiátricos.
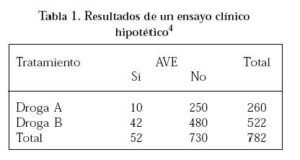
Al analizar esos datos se recibe una reducción absoluta del peligro de 4,2% con 95% de intervalo de confianza de 0,9% a 7,5%. Esto significa que el resultado real, o sea, el resultante al ejercer la participación a la población total de pacientes, está con 95% de probabilidad. Si incrementamos el n de la muestra a 20.000 obtendríamos nuevamente 4,2%, empero con un intervalo de confianza más estrecho, de 3,5% a 4,9%.
Fórmula de intervalo de confianza

Donde:
- p1 Tasa de eventos conjunto 1
- p2 Tasa de eventos conjunto 2
- n1 n conjunto 1
- n2 n conjunto 2
Interpretación de un IC
El intervalo de confianza es una medida de exactitud que posibilita evaluar:
- Si existe diferencia estadística significativa.
- Si tal diferencia es importante para recomendarla.
Para examinar si existe o no diferencia estadística significativa debemos mirar los extremos del intervalo de confianza. Si el estimador puntual muestra beneficio o no, debemos comprobar si alguno de los extremos del intervalo de confianza pasa sobre la línea del no impacto. Si es de esta forma, existe la probabilidad de que el resultado real corresponda al no impacto o inclusive tenga un impacto contrario al deseado. En esta situación no existiría diferencia estadísticamente significativa entre utilizar o no la mediación.
Una vez que un análisis muestra un impacto con importancia estadística, se debería conceptualizar cuál es el beneficio mínimo primordial para recomendarlo.
Así, el análisis hipotético muestra beneficio estadístico importante, siendo el beneficio menor factible de 0,9%. El que este beneficio sea importante es dependiente del tipo de acontecimiento prevenido o favorecido, los efectos adversos de la droga A y droga B. Si el acontecimiento a prevenir es insignificante, o la droga A tiene varios efectos malos y es más cara que B, nuestro umbral será elevado, por consiguiente el beneficio demostrado en nuestro análisis no podría ser importante.
A la inversa, si el acontecimiento a prevenir es importante en sí mismo o si la nueva droga es más barata y sin efectos adversos, quizás con enseñar un resultado de solamente 0,5% nos basta para recomendarla, por consiguiente nuestro análisis no únicamente muestra diferencia estadísticamente significativa, sino que además beneficio importante.
Análisis Gráfico
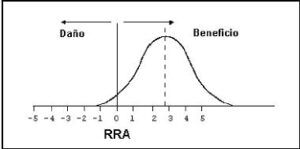
Figura 1.
Análisis hipotético cuyo estimador puntual informa un 2,8%, sin embargo cuyo intervalo de confianza sobrepasa la línea del no impacto. No hay diferencia estadística considerable en este análisis.
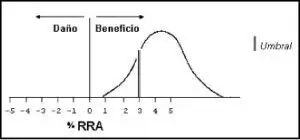
Figura 2.
Se refiere a un análisis hipotético que informa beneficio estadístico, pero el intervalo de confianza pasa sobre el beneficio mínimo primordial para recomendar la terapia (umbral, 3%). El beneficio mínimo demostrado (0,9%) no es suficiente para recomendar la terapia.
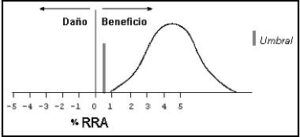
Figura 3.
Análisis hipotético que informa beneficio estadístico importante. El intervalo de confianza no sobrepasa el beneficio mínimo primordial para recomendar la terapia (umbral, 0,5%). El beneficio mínimo demostrado (0,9%) es suficiente para recomendar la terapia.
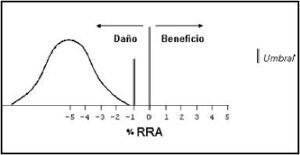
Figura 4.
Análisis hipotético que informa mal estadístico relevante. El intervalo de confianza no sobrepasa el mal mínimo predeterminado como umbral. El mal mínimo establecido es suficientemente fundamental para rechazar la terapia.
