
Son procedimientos estadísticos que estudian la interacción lineal que existe entre 2 variables, la correlación lineal y la regresión lineal. Sin embargo entre ambas existen las siguientes diferencias:
- La correlación como de en relación permanecen 2 variables, mientras tanto que la regresión lineal se basa en producir una ecuación (modelo) que, basándose en la interacción que existe entre las dos variables, que posibilite decir el resultado desde la otra variable.
- El cálculo de la correlación entre 2 variables es sin dependencia del orden o asignación de cada variable a X e Y, mide sólo la interacción entre las dos sin tener en cuenta dependencias. En la situación de la regresión lineal, el modelo cambia según qué variable se considere dependiente de la otra (lo cual no involucra causa-efecto).
- La correlación se usa una vez que ni una de las variables se ha controlado, sencillamente se han medido las dos y se quiere saber si permanecen en relación. En el caso de regresión lineal, es más común que una de las variables se controle (tiempo, temperatura, etc.) y mida la otra.
- Por regla establecida, los estudios de correlación lineal preceden a la generación de modelos de regresión lineal. Primero se examina si las dos variables permanecen correlacionadas y, en caso de estarlo, se proviene a crear el modelo de regresión.
Correlación lineal
Para aprender la interacción lineal que existe entre 2 variables sucesivas se necesita contar con fronteras que permitan cuantificar esa interacción. A esto se refiere la covarianza, que sugiere el nivel de alteración conjunta de 2 variables aleatorias. La fórmula es:
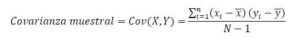
De las escalas en que se miden las variables estudiadas, por consiguiente la covarianza es dependiente, no se compara entre diversos pares de variables. Para lograr hacer comparaciones se estandariza la covarianza, generando lo cual se sabe como coeficientes de correlación. Hay diversos tipos, de entre los que resaltan el coeficiente de Pearson y Tau de Kendall.
Todos ellos varían entre +1 y -1. El 1 es una correlación positiva perfecta y -1 es negativa perfecta. Se emplean como medida de fuerza de agrupación (tamaño del efecto).
Las primordiales diferencias son:
- La correlación de Pearson funciona bien con cambiantes cuantitativas que poseen una repartición habitual. Pese a la carencia de normalidad, es bastante robusto. Es más sensible a los valores extremos que las demás alternativas.
- La correlación de Spearman se emplea una vez que los datos son ordinales, de intervalo, o bien una vez que no se sacia la condición de normalidad para cambiantes sucesivas y los datos pueden cambiar a rangos. Es un procedimiento no paramétrico.
- La correlación de Kendall es otra opción no paramétrica que se utiliza para el análisis de la correlación que usa rangos. Se emplea una vez que se dispone de pocos datos y varios de ellos ocupan la misma postura en el rango, o sea, una vez que hay muchas ligaduras.
Además del costo obtenido para el coeficiente de correlación, se necesita calcular su significancia. Solo si el p-value es importante se puede admitir existente correlación, y esta va a ser del tamaño que indique el coeficiente. Por muy unido que sea el coeficiente de correlación a +1+1 o −1−1, si no es relevante, se ha de interpretar que la correlación de las dos variables es 0, debido a que el costo visto puede ser por fácil aleatoriedad.
El t-test es el examen paramétrico de significancia estadística empleado para el coeficiente de correlación. Al igual que pasa constantemente que se labora con muestras, por un lado está el parámetro preciado (en esta situación el coeficiente de correlación) y por otro su significancia en el momento de tener en cuenta la población completa. Si determinamos el coeficiente de correlación entre X e Y en diferentes muestras de una misma población, el costo cambia dependiendo de las muestras usadas. Por lo cual se calcula la significancia de la correlación obtenida y su intervalo de confianza. La fórmula es:
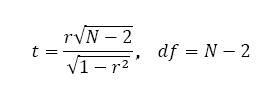
Para este examen de hipótesis, H0 estima que las cambiantes son independientes (coeficiente de correlación de la población=0) en lo que, la Ha, estima existente interacción (coeficiente de correlación de la población ≠0)
La correlación lineal entre 2 variables, además del coeficiente de correlación y de sus significancia, además tiene un tamaño de impacto asociado. Se sabe como coeficiente de decisión R2. Se interpreta como la proporción de varianza de Y explicada por X. En la situación del coeficiente de Pearson y el de Spearman, R2 se recibe elevando al cuadrado el coeficiente de correlación. En el caso de Kendall no se calcula de esta manera.
Coeficiente de Pearson
La covarianza estandarizada es el coeficiente de correlación de Pearson y su ecuación difiere dependiendo de si se aplica a una muestra, Coeficiente de Pearson muestral (r), o si se aplica la población La fórmula del Coeficiente de Pearson es la siguiente:
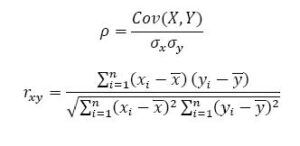
Condiciones
-
- La interacción que se desea aprender entre las dos variables es lineal (de lo opuesto, Pearson no la puede detectar).
- Ambas variables tienen que ser cuantitativas.
- Normalidad: las dos cambiantes se deben repartir de manera común. Diversos textos defienden su solidez una vez que las variables se alejan moderadamente de la regular.
- Homocedasticidad: La varianza de Y sera constante durante la variable X. Esto se concluye si los puntos de vista mantienen la misma dispersión en las diferentes regiones de la variable X.
Características
- Toma valores entre [-1,1], siendo 1 una correlación lineal positiva perfecta y -1 una correlación lineal negativa perfecta.
- Es una medida sin dependencia de las escalas en las que se midan las variables.
- No cambia si se usan transformaciones.
- No posee importancia que las variables sean dependientes o independientes.
- El coeficiente de correlación de Pearson no equivale a la pendiente de la recta de regresión.
Interpretación
Además del costo obtenido para el coeficiente, se necesita calcular su significancia. Solo si el p-value es relevante se puede admitir existente correlación y esta va a ser del tamaño que indique el coeficiente. Por muy unido que sea el costo del coeficiente de correlación a 1 o -1, si no es importante, se ha de interpretar que la correlación de las dos cambiantes es 0 debido a que el costo visto se puede deber al azar.
