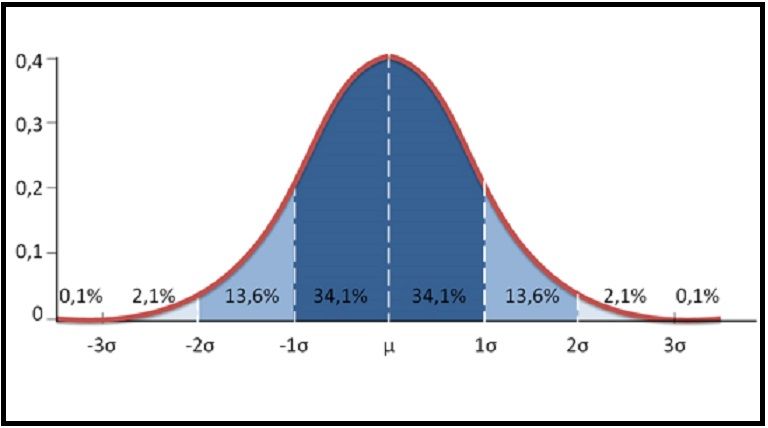
La campana de Gauss es un sistema que se utiliza en estadística y probabilidad. Se conoce como una representación gráfica de la distribución normal de un conjunto de datos. Los que se reparten en valores bajos, medios y altos y conceptuan un gráfico de forma acampanada y simétrica. El punto máximo de la curva indica el promedio y posee dos puntos de inflexión simétricos a derecha e izquierda.
La Campana de Gauss es una función con tres partes especiales: la zona media, en cuyo centro se halla el valor de la media y es cóncava; y los dos extremos, que son convexos y tienden a aproximarse al “eje x”.
El nombre se debe a la grafíca acampanada y simétrica que tiene su función de densidad, que crea que los compendios más comunes son los que están más centrados, mientras que los más raros se emplazan en los extremos.
La Distribución Normal
Ahora vamos a hablar de la distribución Normal. El estudio de la distribución normal lo emprendió de Moivre a finales del siglo XVIII. No obstante toma el nombre de Carl Friedrich Gauss considerado como el matemático más fecundo de la historia, puesto que fue el primero que aplicó esta herramienta, resumidamente, en el análisis de valores astronómicos.
Esta distribución aparece firmemente en la naturaleza o en el modo de las personas. Puesto que representa la conducta de los valores de ciertas variables, cuyas variaciones son influenciadas por fenómenos aleatorios.
La distribución normal es un modelo para aproximar el valor de una variable aleatoria a una situación perfecta de manera adecuada. La distribución normal adapta una variable aleatoria a una función que depende de la desviación típica y la media.
Existen dos tipos de variables aleatorias:
Variable aleatoria continua: toma cualquier número real como por ejemplo el tamaño y el peso o los resultados de una prueba.
Variable aleatoria discreta toma valores naturales como por ejemplo, el número de alumnos de un colegio.
Ejemplo de campana de gauss
¿En qué disciplinas se suele usar? Campos tan diferentes como la biología, psicología, sociología, farmacia o economía, son solo cualesquiera ejemplos de áreas en las que su estudio es esencial.
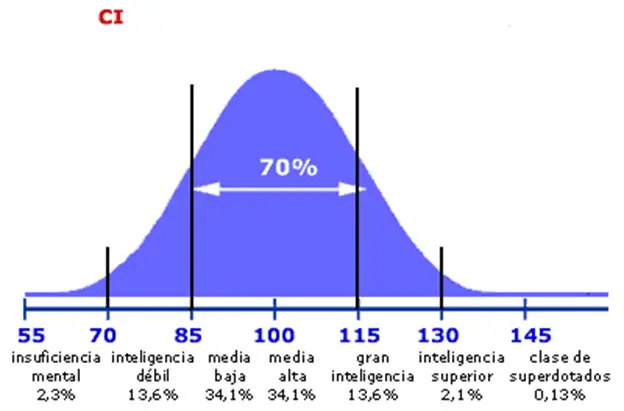
Como ejemplo ilustrativo, veamos una imágen que personifica mediante una Campana de Gauss los datos de losniveles de inteligencia en la población. Vemos que en la campana de gauss la inteligencia media alta representa el centro y los extremos son insuficiencia mental y clase de superdotados respectivamente.
Aplicaciones de la campana de Gauss
¿Y qué aplicación le logramos dar en un entorno digital? En redes sociales como Twitter, Facebook o Pinterest, los usuarios dan asiduamente sus opiniones sobre gustos, datos personales o intereses. Logramos comprobar que esta cantidad enorme de datos, en varios casos, persigue una distribución normal.
Además, una de las ventajas que posee este estudio, es que si experimentamos que una muestra representativa de la población se acerca respecto a un dato a nuestra distribución, la población total estirará a cumplirla, por lo que nos logramos ahorrar el análisis de gran cuantía de datos. Ello conlleva a que de modo muy sencilla, a partir de la muestra poblacional, logramos aproximar de manera muy exacta la cantidad de individuos que conciernen a un cierto intervalo de la variable que estamos estudiando. Como ejemplo, pudríamos aproximar las personas que miden entre 1,70 y 1,80 m. También el número de personas que tienen un pie mayor a la talla 46, sin insuficiencia de tener los datos de todos.
La interpretación de esos valores, logra resultar muy atrayente para empresas de publicidad o de venta de productos. En lugar de realizar un estudio, pueden conocer el número de clientes potenciales precedentemente de lanzar una campaña. De esa forma se puede resolver si les concierne publicitarse en ese medio o no.
¿Cómo se interpreta la campana de Gauss?
La campana de Gauss, también conocida como la curva de Gauss o la distribución normal, se interpreta de la siguiente manera:
- Simetría: La distribución normal es simétrica alrededor de su media (o promedio), lo que significa que la mitad de los datos se encuentran a la izquierda de la media y la otra mitad a la derecha. Esta simetría indica que los valores extremos son menos probables y que los valores cercanos a la media son más probables.
- Pico en la media: La campana tiene un pico en la media, lo que indica que el valor más probable (modo) es igual a la media. En otras palabras, el valor central o esperado de la distribución es la media.
- Dispersión: La anchura de la campana está relacionada con la dispersión o variabilidad de los datos. Una campana más ancha indica una mayor dispersión, mientras que una campana más estrecha implica una menor dispersión. La medida de esta dispersión se representa mediante la desviación estándar.
- Probabilidad acumulativa: El área bajo la curva de la campana representa la probabilidad acumulativa de que una variable aleatoria siga esta distribución y tome valores en un intervalo específico. La mayoría de los valores caen cerca de la media, y la probabilidad de que un valor aleatorio caiga dentro de un cierto rango se relaciona con el área bajo la curva en ese rango.
- Asimetría y curtosis: Además de la simetría, la distribución normal se caracteriza por su asimetría y curtosis (aplanamiento). Una distribución normal perfecta tiene asimetría cero y una curtosis de 3. Las desviaciones de estos valores indican distribuciones que son más o menos asimétricas o achatadas en comparación con la normal estándar.
En resumen, la campana de Gauss es una representación gráfica de la distribución normal y se utiliza para visualizar cómo se distribuyen los datos en una población. La interpretación se basa en la forma característica de la campana y cómo esta forma está relacionada con la media, la dispersión y la probabilidad de los datos.
¿Qué es el área bajo la curva de la campana de Gauss?
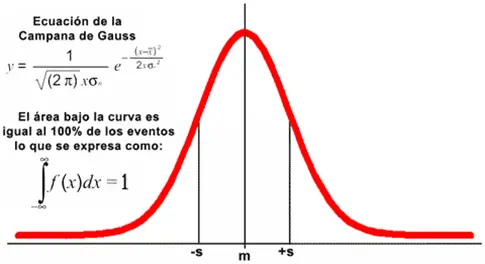
El área bajo la curva de la campana de Gauss es una medida de la probabilidad acumulativa de que una variable aleatoria siga una distribución normal y tome valores dentro de un intervalo específico.
En otras palabras, el área bajo la curva representa la probabilidad de que la variable aleatoria caiga dentro de ese intervalo de valores.
La distribución normal es una distribución continua que se caracteriza por su forma de campana, con un pico en la media y una caída gradual hacia los extremos. El área bajo la curva en un intervalo particular indica qué tan probable es que los valores de la variable aleatoria caigan en ese intervalo.
La probabilidad total bajo la curva de la campana de Gauss es igual a 1, lo que significa que la variable aleatoria debe tomar un valor en algún lugar del rango posible. Para calcular la probabilidad de que la variable esté en un intervalo específico, se integra la función de densidad de probabilidad (PDF) de la distribución normal en ese intervalo.
Por ejemplo, si se quiere saber cuál es la probabilidad de que una variable aleatoria con distribución normal estándar (media igual a 0 y desviación estándar igual a 1) caiga en el intervalo entre -1 y 1, se calcula el área bajo la curva de la campana en ese intervalo. En este caso, la probabilidad sería aproximadamente del 68%, ya que alrededor del 68% de los valores caen dentro de una desviación estándar de la media en una distribución normal estándar.
En resumen, el área bajo la curva de la campana de Gauss es una medida importante en estadísticas que indica la probabilidad de que una variable aleatoria tome valores en un rango específico dentro de una distribución normal. Esta área proporciona información sobre la probabilidad de eventos o resultados en el contexto de la distribución normal.
¿Qué significa gaussiana?
El término «gaussiana» se refiere a algo relacionado con la distribución normal, que también se conoce como la distribución gaussiana en honor al matemático y físico alemán Carl Friedrich Gauss, quien hizo contribuciones significativas a su estudio y comprensión.
La distribución normal es una de las distribuciones más importantes y ampliamente utilizadas en estadísticas y probabilidad. Es una distribución continua que se caracteriza por su forma de campana, con un pico en la media y una caída gradual hacia los extremos. Las características principales de una distribución normal incluyen su simetría alrededor de la media, la relación entre su media y su desviación estándar para describir su forma, y su importancia en modelar una amplia variedad de fenómenos naturales y sociales.
Por lo tanto, cuando se habla de algo como «una distribución gaussiana» o «una función gaussiana», se está haciendo referencia a una distribución o una función que sigue las propiedades y características de la distribución normal o campana de Gauss. En muchos contextos científicos y estadísticos, el término «gaussiano» se utiliza para describir datos o procesos que se asemejan o se modelan adecuadamente utilizando una distribución normal.
¿Cómo se utiliza la distribución normal?
La distribución normal se utiliza en una variedad de aplicaciones en estadísticas, ciencias naturales, ciencias sociales y muchos otros campos debido a su versatilidad y propiedades matemáticas bien comprendidas. Aquí se presentan algunas de las formas más comunes en que se utiliza la distribución normal:
- Modelado de datos: La distribución normal se utiliza para describir y modelar datos continuos que se distribuyen de manera aproximadamente normal, como las alturas de una población, los puntajes en exámenes, el tiempo que tarda en realizarse una tarea, el peso de objetos, entre otros. Cuando los datos se asemejan a una distribución normal, es más fácil realizar análisis estadísticos y hacer inferencias sobre la población.
- Inferencia estadística: La distribución normal es fundamental para la inferencia estadística. Se utiliza para construir intervalos de confianza y realizar pruebas de hipótesis sobre parámetros poblacionales, como la media y la varianza. Estos métodos son esenciales en la toma de decisiones basada en datos.
- Predicción y simulación: En modelos predictivos y simulaciones en campos como la economía, la ingeniería y la física, se asume a menudo que los errores o las variables de entrada siguen una distribución normal. Esto permite realizar predicciones y simulaciones realistas y precisas.
- Control de calidad: En aplicaciones de control de calidad, se utiliza para analizar y controlar la variabilidad en procesos de fabricación y producción. Los límites de control se basan a menudo en distribuciones normales, y se utilizan gráficos de control para identificar desviaciones significativas en los procesos.
- Teoría de la probabilidad: La distribución normal es importante en la teoría de la probabilidad y se utiliza como base para entender otras distribuciones, como la distribución t de Student y la distribución chi-cuadrado, que son cruciales en estadísticas inferenciales.
- Estimación de riesgos y seguros: En finanzas y seguros, se asume que ciertos factores, como los rendimientos de inversiones, siguen una distribución normal. Esto se utiliza en la valoración de activos y la gestión de riesgos.
- Psicometría y psicología: En psicometría, que es la ciencia de la medición psicológica, se utiliza la distribución normal para modelar las puntuaciones en pruebas estandarizadas y evaluar la psicología de las poblaciones.
En resumen, la distribución normal es una herramienta fundamental en estadísticas y ciencias debido a su capacidad para modelar y describir datos en una amplia gama de campos. Se utiliza para realizar análisis, inferencias, predicciones y toma de decisiones basadas en datos, y su comprensión es esencial para cualquier persona que trabaje con datos y estadísticas.
