El valor p es una noción muy fácil de concebir pero que por alguna razón, lastimosamente, no se explica bien, o derechamente ni se explica. Es una malo porque posiblemente sea esa la razón de que únicamente realicen bien los ejercicios de contraste aquellos que poseen mejor memoria que otros y se tengan podido instruirse la regla, menor que α rechazo, mayor que α no rechazo.
En mi dictamen, si ambicionamos que se comprenda el sentido de formar un contraste de hipótesis, hay que exponer este tipo de nociones que son los que al fin y al cabo poseemos que traer para tomar una decisión y para dar una respuesta. No le veo sentido a poseer estudiantes que anden la asignatura y no sepan qué es el valor p.
A continuidad una manera resumida de concebirlo es la siguiente.
Lo primero que hay que comprender es que el valor p es una probabilidad. Por lo tanto esta entre 0 y 1, y jamás estará fuera de ese rango. Esto lo digo porque veremos esta notación, por ejemplo, un valor p= 136.98e-5. Esta notación es igual a 136.98 * 10^(-5), lo que viene siendo igual a 0.0000013698. Ese «e-5» significa que debemos multiplicar ese número de 136.98 por diez elevado a cinco, y se crea así para evitar colocar un signo largo.
El del ejemplo no es muy largo pero conjeturara que coloco 136.98e-50 = 136.98 * 10^(-50). Entonces poseeríamos varios ceros, así que mejor acostumbrarnos a usar la notación científica.
Esto vale cantidad para un exponente negativo (que figura que el número es muy pequeño). Como para un exponente positivo (que figura que el número es más grande). Aquí tienes algunos ejemplos:
Ejemplos valor p
69800000 = 6.98*10^8
42000 = 4.2*10^4
Volviendo al valor p, vivimos de acuerdo en que es una probabilidad y que su valor eternamente estará entre 0 y 1. Yo lo puedo precisar en una sola frase, pero no me gusta expresar nada más principiar porque si no mis alumnos se quedan con la frase y se olvidan del por qué. Así que si de verdad quieres concebir el trasfondo, quédate aquí que yo te lo expongo.
Vamos a suponer que poseemos un contraste de hipótesis. ¿Qué es un contraste de hipótesis? Si no estar al corriente esto no creo que poseas dudas con relación al p-valor, voy a reflexionar que ya sabes lo más básico del tema de contrastes de hipótesis, qué es la hipótesis nula y la disyuntiva.
Conjeturemos que estamos haciendo inferencia sobre la media poblacional, y poseemos un contraste de hipótesis unilateral por la derecha. Esto es cuando la hipótesis nula (H0) nos dice que la media poblacional es menor o igual que µ0 y la hipótesis dilema (lo que se sospecha) nos dice que es mas que ese valor µ0.
Contraste unilateral a la derecha
El primer paso en aquel tiempo es igualar el tipo de contraste y sobre qué parámetro. En este caso es sobre la media, así que traemos como estadístico una expresión donde va a estar la media muestral, la media poblacional (µ0) y otras cosas como el tamaño muestral (n) y la desviación típica poblacional.
El subsiguiente paso es hallar el valor experimental de ese estadístico, sustituyendo la información muestral (media muestral y tamaño muestral). Si no vemos la desviación típica poblacional logramos usar la cuasidesviación típica muestral en caso de que no poseamos más de 30 datos, y abandonaremos de tener a la distribución Normal, ahora poseeremos una t-Student con n-1 grados de libertad. Pero teniendo más de 30 datos podemos seguir utilizando la Normal por el Teorema Central del Límite.
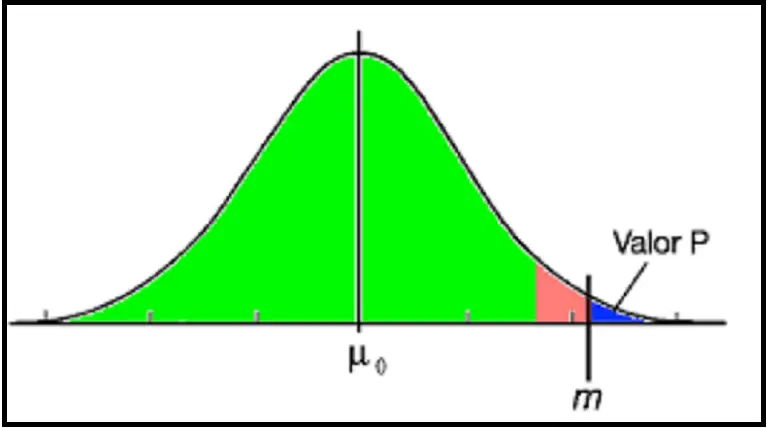
Resumiendo, conjeturemos que poseemos el caso más sencillo, marchamos a conjeturar que podemos usar la Normal porque poseemos suficientes datos, que tenemos toda la información disponible, calculamos ese valor experimental del estadístico de contraste, y como nuestro contraste es unilateral a la derecha, lo que vamos a hacer es hallar la probabilidad a través de la normal a la derecha de ese valor de experimento. Esa probabilidad va a ser el valor p.
¿Qué es la región de rechazo?
La región de aceptación, es donde se obtiene el valor de rechazo.
Entonces, en este ejemplo la conclusión sería: No rechazamos la hipótesis nula H0.
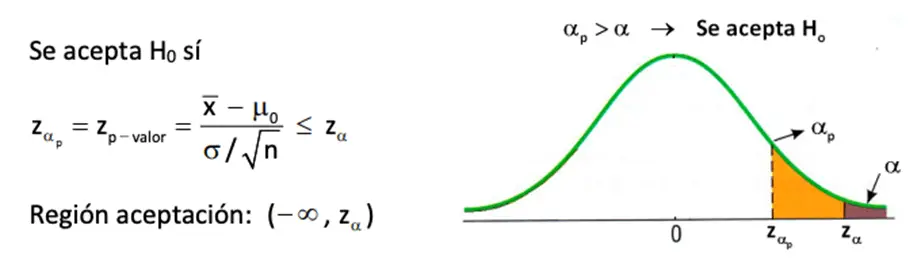
Advertirás ahora algo muy atrayente, da igual si cotejas el valor p con el α, o si comparas z_α_p y z_α. Ambas conveniencias te van a llevar a una única conclusión. Porque si el p-valor es mayor que α, quedamos en un caso similar al del ejemplo, eternamente va a ser porque el área del p-valor es mayor que el área α. Y esto quiere decir que z_α_p va a estar en la región de aceptación, no la de rechazo.
En aquel tiempo, logramos decir que si el p-valor es adecuadamente grande, más grande que el nivel de significación α, no vamos a rechazar la hipótesis nula.
Y si, por el contrario, el p-valor es suficientemente pequeño, menor que el nivel de significación α (que suele ser de por sí bastante pequeño: usualmente 0.05), sí vamos a rechazar la hipótesis nula.
¿Cómo podemos interpretar entonces el p-valor?
El p-valor es por tanto una fuerza de la muestra en los datos en contra de H0. Pero más pequeño sea el valor p, más concreta será la evidencia de la muestra para rechazar H0. Mientas menor sea el valor p, menos vamos a creer en la hipótesis nula y la culminaremos rechazando.
