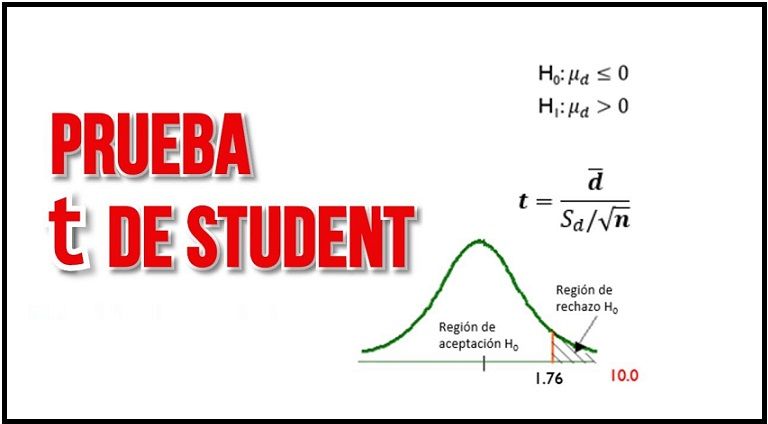
Prolongando con la serie de entradas sobre los disparejas test estadísticos, en este post vamos a estudiar la prueba «t» de Student.
¿Qué hay que saber de la «t» de Student?
Se maneja para establecer si hay una discrepancia significativa entre las medias de dos grupos, es decir que se utiliza cuando deseamos comparar dos medias.
Se maneja para la comparación de dos medias de poblaciones independientes y normales.
Tomamos que las variables dependientes poseen una distribución normal.
Detallamos el nivel de la probabilidad (nivel de la alfa, nivel de la significación, p) que quedamos preparados a aceptar (p < .05 es un valor común que se utiliza).
- Con una prueba t, poseemos una variable independiente y una dependiente.
- La variable independiente solo puede tener dos niveles (joven y mayor).
- Si la independiente asumiera más de 2 niveles, posteriormente manejaríamos un análisis de la variación unidireccional (ANOVA).
- La prueba estadística para t de Student es el valor t. Conceptualmente, la t-valor incorpora el número de unidades estándares que están apartando las medias de los dos grupos.
- Si nuestra t-prueba causa una t-valor que da lugar a una probabilidad de .01, expresamos que la probabilidad de lograr la diferencia que hallamos sería por casualidad de uno de cada cien veces.
4 factores ayudan para indicar si la discrepancia entre dos medias de los grupos se puede reflexionar significativa:
- Cuanto mayor es la discrepancia entre las dos medias, mayor es la probabilidad que una diferencia estadística significativa coexiste.
- El tamaño de la muestra es extremadamente significativa en la determinación de la significación de la discrepancia entre las medias. Acrecentando el tamaño de la muestra, las medias extienden a ser más estables y más representativas.
- Un nivel más grande de la alfa solicita menos diferencia entre las medias (p <0 font=»font»>.05).
- Se debe manejar una hipótesis (con dos colas) no directivas.
Asunciones subyacentes la prueba de t:
- Las muestras se han dibujado aleatoriamente a partir de sus poblaciones respectivas.
- La población se debe distribuir regularmente.
- Unimodal (un modo).
- Simétrico, lo mismo existe arriba y abajo de la media.
- Acampanado (cuando la moda se encuentra en el medio).
- Media, moda, y mediana se restringen en el centro.
- Asintótico (en cuanto más lejos se aparta la curva de la media, más colindante será el eje de X; pero la curva jamás debe tocar el eje de X).
- El número de individuos en las poblaciones debe poseer la misma varianza (s2 = s2).Si no es el caso se maneja otro cálculo para el error estándar.
Existen 2 tipos de prueba t de Student
Test t para diferencia par (grupos dependientes, test t correlacionado): df= n (número de pares) -1
Esto se describe a la diferencia entre las cuentas medias de una sola muestra de individuos que se establece antes del tratamiento y después del tratamiento. Puede asimismo comparar las cuentas medias de muestras de individuos que se aparean de indiscutible manera (por ejemplo los hermanos, hijas, etc).
Test t para muestras independientes
Esto se cuenta a la diferencia entre los promedios de dos poblaciones.
Fundamentalmente, la manera compara los promedios de dos muestras que existieron apartadas independientemente una de la otra.
Un ejemplo sería cotejar cuentas matemáticas de un grupo experimental con un grupo de control.
¿Cómo resuelvo qué tipo de t-prueba a manejar?
Error tipo I:
- Rechaza una hipótesis nula que sea verdaderamente verdad. La probabilidad de crear un error tipo I depende del nivel alfa que se eligió.
- Si se fijó la probabilidad alfa en p < 05, entonces consta un 5% de posibilidades de hacer un error de tipo I.
- Se logra reducir la posibilidad de hacer un error tipo I fijando un nivel alfa más pequeño (p < .01). El problema creando esto es que se acrecienta la posibilidad de un error tipo II.
Error tipo II:
- Falla en refutar una hipótesis nula que sea falsa.
- La idea básica para computar una prueba de Student es hallar la diferencia entre las medias de 2 grupos y dividirla por el error estándar de la diferencia. Lo que significa la desviación de estándar de la distribución de las diferencias.
- Un intervalo de confianza para una prueba t con 2 colas es computado multiplicando los valores críticos por el error de estándar y añadiendo y restando eso de la diferencia de las dos medias.
- El resultado tamaño se maneja para calcular la discrepancia práctica. Si coexisten varios miles de pacientes, es muy fácil hallar una diferencia estadísticamente significativa
- Estar al corriente si esa diferencia es práctica o significativa es otra interrogación.
- Con los estudios implicando diferencias de grupo, el tamaño de la consecuencia es la diferencia de las dos medias dividido por la desviación estándar del grupo control.
- Universalmente, el tamaño de la consecuencia es simplemente importante si consta una significación estadística.
- Un efecto tamaño de 2 se medita pequeño, 5 se reflexiona medio, y 8 se imagina grande.
