
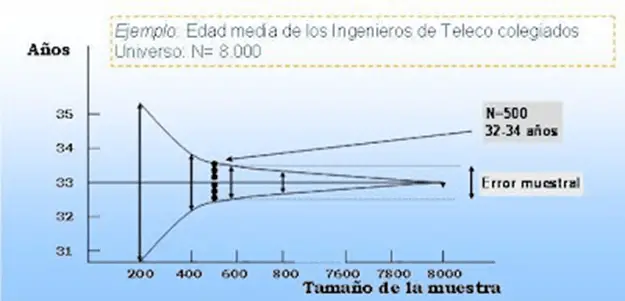
El error muestral es el error grande estadístico de la muestra, válido para el conjunto de todas las diferentes muestras que se logran tomar de la equivalente población.
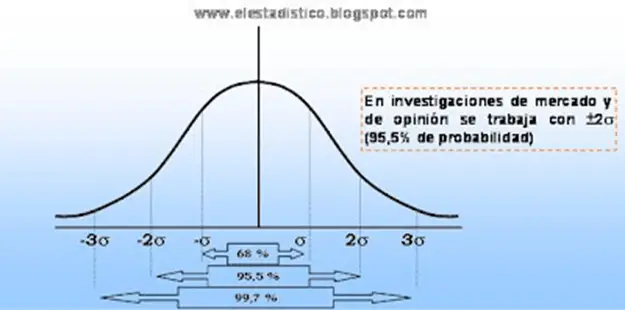
Las pruebas empíricas ejecutadas muestran que la distribución de las medidas de las muestra probables del mismo tamaño en una población se concuerda por lo corriente a la ley normal de probabilidad (campana de Gauss).
Margen de Confianza o Nivel de Significancia
- De cada cien potenciales muestras del universo 68% (± s), o 95,5% (±2s), o 99,7% (±3s) van a poseer el promedio muestral igual que al del universo.
- El margen de confianza es la porción de la distribución gaussiana (medida en unidades ± s) que nos planteamos realmente utilizar, es decir es la probabilidad de que una estimación (resultado muestral) se ajuste al contexto (resultado censal o del universo).
Intervalo o margen de confianza de 1 variable es igual a: Indicador promedio ± Error muestral
Nivel de Confianza que son utilizadas únicamente para variables de intervalo: Nº de s
Fórmula del Error Muestral
El error muestral obedece:
- De la amplitud del universo (N).
- Capacidad de la muestra (n).
- De la desviación típica (s) en variables de intervalo y razón.
- Variabilidad (p*q) en variables nominales y ordinales.
El cambio de una variable nominal u ordinal se debe a lo siguiente:
- Juega un igual papel que la varianza s² en las variables del intervalo.
- Una variable nominal o una ubicación en una escala (variable ordinal)
muestra una proporción (p) de la población frente a lo demás (q=1-p). - Podemos presentar la proporción como una variable booleana.
Ejemplo: Distribución de algunas variables por género
Humanidad…………Hombres (p=60%)…..Mujeres (q=40%)…Variabilidad (p*q=2400)
Matemáticas……….Hombres (p=80%)…..Mujeres (q=20%)…Variabilidad (p*q=1600)
Física………………Hombres (p=0%)..Mujeres (q=100%)……Variabilidad (p*q=0)
Formulas del error:
Población infinita (N>100.000 ) Población finita
De intervalo: E=(s²/n)½ E=((s²/n)·((N-n)/(N-1)))½
De proporción: E=((p·q)/n)½ E=((p·q/n)·((N-n)/(N-1)))½Donde:
- E es el error muestral el cual es usado en unidades s.
- N ser refiere al Universo.
- n se refiere a la muestra.
- La estimación del error tiene relación con el nivel de confianza:
- ERROR= E · nivel de confianza elegido (nº de unidades s )= E · s
