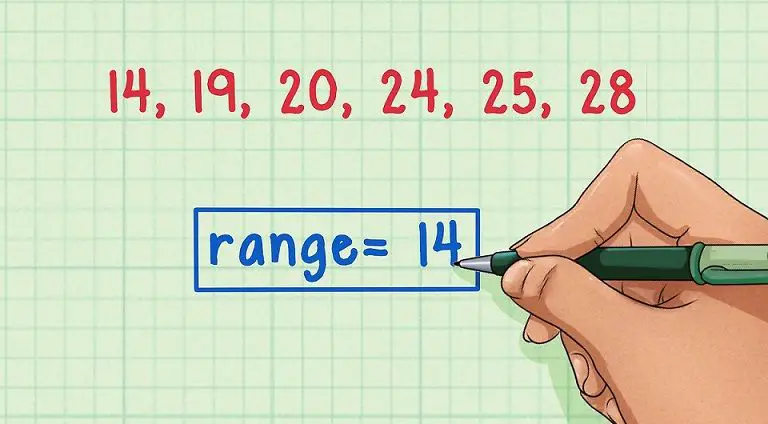
Existen muchas ventajas y desventajas del rango en estadistica. El rango es un parámetro manejado para diversificar el valor máximo y mínimo de una muestra característica. Asimismo se maneja para estudiar variaciones y lograr la dispersión total de una explícita muestra.
Como se mencionó anteriormente, el rango en estadística se utiliza para revelar cuán cercanos o distantes están los datos de una determinada muestra. El hecho de calcular el rango, implica muchas ventajas, destacando:
Ventajas y desventajas del rango en estadistica
Ventajas del rango
- Es muy sencillo de calcular, debido a que se trata de una sustracción o resta.
- Para los observadores es muy fácil captarlo.
- Se utiliza no solo en la estadística, sino en otras ramas como la ingeniería.
- Ayuda a determinar las desviaciones o distorsiones estándar.
- Su interpretación es intuitiva.
A pesar de que el rango en estadística, ayuda a determinar muy bien el valor máximo y mínimo de una población, cuenta con desventajas en su metodología, algunas dadas por:
Desventajas del rango
- El concepto es corriente, solo da una idea de cuán amplio es el intervalo entre el valor máximo y mínimo de una muestra.
- Utiliza solo valores extremos, desconociendo los valores medios.
- Nunca disminuye, a pesar de que se aumenten otros datos, el rango extiende a extenderse o persistir igual.
Todo lo mencionado son las principales ventajas y desventajas del rango en estadistica.
¿Cuál es el rango en estadística?
El rango, asimismo conocido como amplitud o recorrido estadístico, es un valor numérico que revela ágilmente la diferencia entre el valor máximo y mínimo; es decir, la extensión del intervalo que coexiste entre ellos. Este proceso logra ser utilizado en cualquier muestra estadística para lograr la dispersión absoluta.
Mientras más pequeño sea el rango, la distancia que preexiste entre los datos es poca. Caso contrario cuando el rango es más grande, ya que mostrará que están más distanciados. Asimismo, es muy útil en el área de finanzas, ya que les auxilio indicando que tan grande podrían ser las variaciones.
Si bien es cierto que manejando este método lograremos un cálculo más rápido realizando un método sencillo, correspondemos poseer en cuenta que en variadas momentos la medida del rango no es exacta, debido a que una gran parte de la averiguación es ignorada, así que no se sabe cómo los datos que contiene la muestra se reparten.
Su uso se encomienda para muestras pequeñas, ya que es más eficiente. Para lograr una idea con mayor precisión del grado de dispersión, es superior emplear otros métodos estadísticos, como la desviación estándar o la varianza.
¿Cuáles son las tipos del rango en estadística?
El rango es un parámetro manejado para obtener el intervalo entre el valor máximo y mínimo de una explícita población o muestra. Diferenciar el rango de otros parámetros, es muy sencillo. Sin embargo a continuación te mostramos las características de este:
- Es manejado para tener una suposición del grado de separación que hay dentro de un conjunto de datos.
- Tiene una unidad de medida equivalente a las investigaciones.
- No es muy preciso.
- Se basa únicamente en los valores extremos, lo que logra provocar que la información de la dispersión que contribuye esté distorsionada.
- El valor del rango varía cuando cada observación del vinculado de datos es multiplicado por una constante K.
- El valor del rango no se altera cuando cada observación del conjunto de datos es sumada con una constante
- Es el método más natural que brinda resultados apresurados.
- El recorrido, factor significativo del rango, es la mesura más fácil de calcular, completo a que se trata simplemente de la distancia de los valores extremos.
Ecuación del Rango en estadística
En estadística, el rango hace referencia al recorrido o amplitud, entre los conjuntos de datos máximos y mínimos de una determinada muestra. Asimismo se dice, que el rango es la diferencia entre los valores antes mencionados.
La ecuación aplicada universalmente suele tener ciertas restricciones, una de ellas es que el rango suele ser personificado con “R” y las variables mediante “X”. Por ejemplo:
R=MAX – MIN
Donde:
- “Máx” es el valor más grande que se exhibe en la muestra.
- “Mín” es el valor más pequeño que se exhibe en la muestra.
Antes de manejar la fórmula y refiriendo con el conjunto de valores, se encomienda que se ordene los números según su tamaño para más habilidad; pero si logramos identificar ágilmente sin necesidad de ordenarlos, a la sazón pasemos de esto.
Ejemplos de rangos en estadística
La concepción del rango se adapta afinadamente a la de medida de dispersión sencilla, ya que la medida de dispersión o variabilidad entre intervalos se logra diferenciar expeditamente. Sin embargo, el rango en estadística se contrasta a continuación en los ejemplos:
Para una muestra de datos (3, 2, 4, 4, 8) el valor mínimo es 2, y el valor máximo es 8. Calcular el rango.
R=8-2=6
Para una muestra de datos (14, 6, 19, 8) el valor mínimo es 6, y el valor máximo es 19. Calcular el rango.
R=19-6=13
Para una muestra de datos (12, 11, 14, 4) el valor mínimo es 4, y el valor máximo es 14. Calcular el rango.
R=14-4=10
