En todo estudio estadistico se pueden usar distintas medidas descriptivas que representan las características de tendencia central, entre los que tenemos están la media mediana y moda. Si se calculan desde una muestra de datos, se les nombra estadísticos; si se les calcula desde una población se les llama fronteras.
La mayoría de los conjuntos de datos presentan una tendencia a agruparse cerca de un punto central (media mediana y moda) y en la mayoría de los casos es viable escoger cualquier costo que describa todo un grupo de datos.
Un valor utilizado frecuentemente es una medida de tendencia central (media mediana y moda). Son conocidas como medidas de tendencia central la media mediana y moda.
Media aritmética
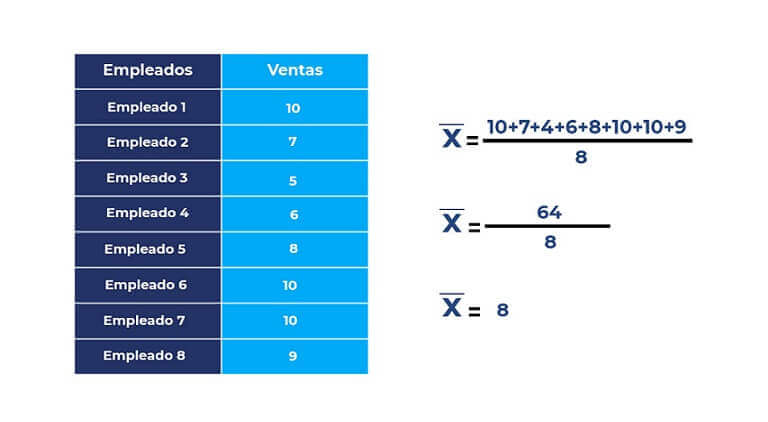
La media aritmética es el tamaño de tendencia central que se usa con más frecuencia. Se calcula sumando cada una de las visualizaciones de un grupo de datos, dividiendo luego aquel total entre el número total de recursos relacionados.
La media aritmética de un grupo de valores se define como el cociente entre la suma de los valores y el número de ellos. Se escribe como x si la media aritmética es de una muestra y µ si la media aritmética es poblacional.
Las características e incovenientes de la media son:
Características de la media
- La media aritmética es el punto de equilibrio o centro de gravedad del reparto, es decir, la suma de las desviaciones de todos los valores de la variable con respecto a la media es igual a cero.
- En el cálculo de la media se utiliza toda la información contenida en el reparto de frecuencias.
- La media de un valor que no cambia es la misma constante.
- Si a todas las observaciones de la variable, X, se le aplica una transformación del tipo X’=a+bX, la media de la variable transformada X’ se puede calcular en funcionalidad de la media de X, siendo X’=a +bX.
- Si se divide el reparto en submuestras disjuntas y exhaustivas, la media del reparto se puede calcular a partir de las medias de las submuestras ponderando estas últimas por el número de recursos que contienen.
Inconvenientes de la media
- Sólo se puede obtener si la característica vista es cuantitativa.
- La media es bastante sensible a la vida de observaciones extremas, tendiendo a desplazarse hacia éstas. Cuando esto pasa la media no sintetiza de forma correcta el reparto de la variable. En estos casos puede calcularse la media recortada.
Tipos de datos para calcular la media
-
Para datos no agrupados:
Ejemplo: Calcular la media aritmética con las notas de examen en Estadística conseguidas por un cierto estudiante.
-
Para datos agrupados:
Si los datos permanecen ordenados en tablas de frecuencia la media aritmética se recibe como sigue
donde:
xi se conoce a la marca de clase del intervalo i-ésimo
fi se conoce a la frecuencia del intervalo i-ésimo
n se dice al número de datos de la muestra
N se dice al número de datos poblacional
m es el número de intervalos
Ejemplo: Cual es la media aritmética para el peso los trabajadores según la tabla:
| Peso (Kg.) | xi | fi | xifi |
| 55 – 62 | 58,5 | 5 | 292,5 |
| 63 – 70 | 66,5 | 15 | 997,5 |
| 71 – 78 | 74,5 | 12 | 894 |
| 79 – 86 | 82,5 | 5 | 412,5 |
| 87 – 94 | 90Á 5 | 3 | 271,5 |
| Total | 40 | 2868 |
El peso es de 72 kilogramos de los trabajadores, es decir la media obtenudi de dividir 2868/40=72
Propiedades de la media aritmética
Propiedad 1 La misma constante es la media aritmética de una constante.
Propiedad 2 La media aritmética de una variable más una constante es el mismo valor que la suma de la media aritmética de la variable y la constante.
Tercera propiedad La media aritmética de una variable por una constante es equivalente al producto de la constante por la media de la variable.
Ventajas y desventajas de la media aritmética
Las principales ventajas y desventajas son:
| Ventajas | Desventajas |
| – Se muestra estable | – No se aplica a atributos |
| – Fácil interpretación y cálculo | – Los valores extremos influyen en su valor |
Mediana
La mediana está dentro de una sucesión ordenada de datos. No se ve afectada por visualizaciones extremas en un grupo de datos. Cuando se muestra alguna información extrema, resulta apropiado usar la mediana en vez de la media para explicar el grupo de datos. Su signo es Me.
Las carcterísticas e incovenientes de la mediana son:
Características de la mediana
- En las mismas unidades de medida de la variable la mediana se expresa .
- Modifican la mediana, los cambios de origen y de escala.
- La mediana puede ser una medida de tendencia central más representativa que la media cuando la variable muestra valores extremos.
Inconvenientes de la mediana
- Si la característica vista es ordinal, sólo en ese caso se puede obtener.
- En el cálculo de la mediana no se tiene presente toda la información contenida en el reparto de frecuencias.
- Depende de la forma en que se presente la ordenación de los datos, el procedimiento a seguir para localizarla: Stem and leaf, tabla de frecuencias principales, tabla de frecuencias con los valores agrupados en intervalos.
- La mediana es el valor de la variable correspondiente a la postura que deja tantas observaciones por debajo como por encima, con la ordenación de los recursos de la muestra proporcionada por el diagrama Stem and leaf. Si el número de observaciones es n la postura central es (n+1)/2 y la mediana es el precio que ocupa dicha postura. Si el número de observaciones es par, la mediana se calcula como el promedio de los valores de la variable correspondiente a los dos recursos centrales.
- Con los valores dispuestos en una tabla de frecuencias simple, la mediana es el precio al que corresponde la primera frecuencia absoluta acumulada más enorme o igual que n/2
- Una vez que los valores de la variable se agrupan en intervalos, el intervalo que tiene a la mediana es el primero que muestra una frecuencia absoluta acumulada igual o superior a n/2. Una vez localizado el 2 intervalo mediano, el precio de la mediana se aproxima mediante la siguiente fórmula basada en el supuesto de que la frecuencia correspondiente a cada intervalo se distribuye uniformemente en éste.
Siendo Limites:
Tipos de datos para calcular la mediana
-
Mediana para datos no agrupados
Se tienen que ordenar los datos de manera creciente o decreciente. Para muestras con un número par de visualizaciones, la mediana es el dato que queda en el interior de esa ordenación y para muestras con número impar de visualizaciones la mediana es el promedio de ambos datos centrales.
Ejemplos de la mediana:
Ejemplo 1 Para la muestra de numero impar de datos Mediana=(Xn +1)/2
datos: 4,7,5,6,3,2,7
ordenando los mismos: 2,3,4,5,6,7,7. Como son 7 datos se elije el dato 4 por lo tanto la mediana es X4=5
Ejemplo 2 Para la muestra de numero par de datos Mediana=(X(1/2)+X(1/2+1))/2
datos: 12,15,14,16,11,10,10,13
ordenando los mismos: 16,15,14,13,12,11,10,10. Como son 8 datos se elijen los datos 4 y 5 y se obtiene un promedio de los mismos por lo tanto la mediana es X=12,5
donde:
ni: es el primer intervalo cuya frecuencia acumulada supera a n/2
Li: límite inferior
n: es el número de datos.
Fi-1: al intervalo de la mediana, es la frecuencia acumulada anterior.
fi: del intervalo de la mediana es la frecuencia absoluta.
a: es la amplitud del intervalo.
Moda
La moda es en un grupo de datos el valor que surge con más frecuencia. La moda no se vee afectada frente a la ocurrencia de valores extremos. Se usa la moda para fines descriptivos para diversas muestras. Su signo es Mo.
Las características e incovenientes de la moda son:
Características de la moda
- En las unidades de medida de la variable se expresa.
- La moda es la única medida de postura que sintetiza el reparto de frecuencias de una característica categórica nominal.
Inconvenientes de la moda
- Puede tener más de una moda, una distribución de frecuencias.
- No se tiene presente toda la información contenida en el reparto de frecuencias para implantar la moda.
Para localizar la moda se busca la frecuencia (absoluta o relativa) máxima, el precio de la variable correspondiente a dicha frecuencia es la moda.
Si se agrupan en intervalos los valores de la variable, el intervalo modal corresponde a la frecuencia máxima. En tal caso puede tomarse la marca de clase del intervalo modal como precio aproximado de la moda.
Ejemplos de la moda
Ejemplo de moda unimodal
¿Cuál es la moda del siguiente conjunto de datos?
5,4,9,7,2,3,9,6,5,2,5
Los números están desordenados, por lo que primero los ordenaremos para que sea más fácil encontrar la moda.
2,2,3,4,5,5,5,6,7,9,9
Los números 2 y 9 aparecen dos veces, pero el número 5 está repetido tres veces. Por lo tanto, la moda de la serie de datos es el número 5.
Mo=5
Ejemplo de moda bimodal
Calcula la moda del siguiente conjunto de datos:
8,7,0,6,10,9,13,8,0,6,2,6,5,11,10
0,9,8,6,12,3,5,11,1,4,8,10,2,5,7
Primero ponemos los números en orden:
0,0,0,1,2,2,3,4,5,5,5,6,6,6,6
7,7,8,8,8,8,9,9,10,10,10,11,11,12,13
Como puedes comprobar, el número 6 y el número 8 aparecen un total de cuatro veces, el máximo número de repeticiones. Por lo tanto, en este caso se trata de una moda bimodal y ambos números son la moda del conjunto de datos:
Mo={6;8}
Medidas de localización
Cuantiles
Si se catalogan los recursos de la muestra desde el que tiene el menor precio de la variable hasta el que tiene el más enorme precio, los cuantiles son los valores de la variable que dividen al reparto en un cierto número de partes con igual número de recursos.
Los cuantiles estan en las unidades de la variable, siendo los más utilizados los cuartiles, deciles y centiles.
Cuartiles
Son los 3 valores de la variable, Q1, Q2, Q3 que dividen el reparto en 4 partes con igual número de observaciones.
El primer cuartil, Q1, es el precio de la variable que deja por debajo el 25% del total de observaciones. El segundo cuartil, Q2, es el precio de la variable que deja por debajo el 50% de las observaciones y, por lo tanto, coincide con la mediana. El tercer cuartil, Q3, es el precio de la variable que deja por debajo el 75% del total de observaciones.
Entre 2 cuartiles continuos está el 25% del total de observaciones.
El cuartil es el precio de la variable al que le corresponde la primera frecuencia absoluta acumulada más enorme o igual que kn dónde k= 0,25 para Q1; k=0,5 para Q2 y k= 0,75 para Q3.
Si los valores de la variable se agrupan en intervalos, el intervalo que tiene al cuartil es aquel cuya frecuencia absoluta acumulada es la primera más enorme o igual que kn.
Una vez situado el intervalo que lo tiene, el precio de Qi se aproxima mediante la siguiente fórmula basada en el supuesto de que la frecuencia correspondiente a cada intervalo se distribuye uniformemente en éste.
Deciles, Centiles o Percentiles
Los decíles son los 9 valores de la variable, D1, D2, …., D8, D9 que dividen el reparto en 10 partes con igual número de observaciones.
El D1, es el valor de la variable que tiene por debajo el 10% de las observaciones; el D2 es el valor de la variable que deja por debajo el 20% de las observaciones y así sucesivamente. El D5 es igual que la mediana.
Entre 2 deciles continuos está el 10% del total de observaciones.
Los Centiles o Percentiles son los noventa y 9 valores de la variable, C1, C2, …., C98, C99 que dividen el reparto en cien partes con igual número de observaciones.
El primer C1 es el valor de la variable que deja por debajo el 1% de las observaciones; el 2 centil, C2, es el precio de la variable que deja por debajo el 2% de lo visto. El 50 centil es el mismo que la mediana.
Entre 2 centiles consecutivos está el 1% del total de observaciones.
Su cálculo es parecido al de los cuartiles. Una vez ubicado el intervalo, el precio aproximado del cuantil es:
Es k=0.1;0.2,etc para deciles y k=0.01, 0.02,etc para centiles.
