Los cuartiles son una instrumento que utilizamos en la estadística. El calculo de cuartiles vale para administrar grupos de datos previamente ordenados.
Los cuartiles son los 3 elementos de la variable que dividen a un conjunto de datos sistemáticos en cuatro partes iguales.
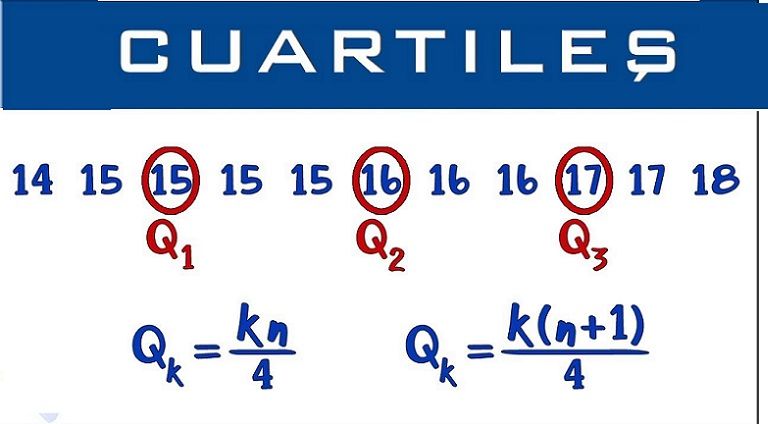
Q1, Q2 y Q3 determinan los valores correspondientes al 25%, al 50% y al 75% de los datos. Q2 coincide con la mediana.
Para poder realizar el calculo de cuartiles ordenamos los datos de menor a mayor y buscamos el lugar que ocupa cada cuartil mediante la expresión (k*N/4)=1,2,3.
Número impar de datos
2,5,3,6,7,4,9
2,3(Q1),4,5(Q2),6,7(Q3),9
Número par de datos
2,5,3,4,6,7,1,9
1,2,3,4,5,6,7,9
2,5 (Q1)
4,5 (Q2)
6,5 (Q3)
Calculo de cuartiles para datos agrupados
Inicialmente buscamos la clase donde se encuentra k*N/4=1,213 , en la tabla de las frecuencias acumuladas.
Qk= Li + ((k*N/4 – Fi-1)/fi)*ai
Li es el límite inferior de donde está el cuartil.
N es la suma de la totalidad de las frecuencias absolutas.
Fi-1 es la frecuencia acumulada primera al tipo del cuartil.
ai es la amplitud del tipo
Ejemplo de ejercicio de calculo de cuartiles
Deducir los cuartiles de la distribución de la tabla:
| fi | |
| 50,60 | 12 |
| 60,70 | 10 |
| 70,80 | 16 |
| 80,90 | 14 |
| 90,100 | 10 |
| 100,110 | 5 |
| 110,120 | 2 |
En primer lugar estableceremos un evento columna con los valores de la frecuencia acumulada:
En la 1 casilla ponemos la primera frecuencia absoluta.
En la 2 casilla sumamos el valor de la frecuencia acumulada 1 y la frecuencia absoluta conveniente y así continuamente hasta la última, que posee que ser igual a N=69
| fi | Fi | |
| 50,60 | 12 | 12 |
| 60,70 | 10 | 22 |
| 70,80 | 16 | 38 |
| 80,90 | 14 | 52 |
| 90,100 | 10 | 62 |
| 100,110 | 5 | 67 |
| 110,120 | 2 | 69 |
Cálculo del primer cuartil
Investigamos el intervalo donde se halla el uno cuartil, multiplicando 1 por N=69 y realizando la división por 4.
69*1/4=17,25
Investigamos en la columna de las frecuencias acumuladas Fi el intervalo que sujeta a 17.25.
La clase de Q1 es: 60,70
Emplearemos la fórmula para el cálculo de cuartiles para datos agrupados, eliminando los sucesivos datos:
Li=60
Fi-1=12
Fi=10
ai=10
Q1= 60 + ((17,25-12)/10)*10=65,25
Cálculo del 2 cuartil
Averiguamos el intervalo adonde se halla el segundo cuartil, multiplicando 2 por N=65 y dividiendo por 4.
69*2/4=34,5
Investigamos en la columna de las frecuencias acumuladas Fi el intervalo que sujeta a 34.5.
La clase de Q2 es: 70,80
Emplearemos la fórmula para el cálculo de cuartiles para datos agrupados, eliminando los sucesivos datos:
Li=70
Fi-1=22
Fi=16
ai=10
Q2= 70 + ((34,5-22)/16)*10=77,81
Cálculo del 3er cuartil
Investigamos el intervalo donde se encuentra el tercer cuartil, multiplicando 3 por N=69 y dividiendo por 4.
69*3/4=48,75
Averiguamos en la columna de las frecuencias acumuladas Fi el intervalo que sujeta a 48,75
La clase de Q3 es: 80,90
Emplearemos la técnica para el cálculo de cuartiles en valores agrupados, eliminando los datos:
Li=80
Fi-1=38
Fi=14
ai=10
Q3= 80 + ((48,75-38)/14)*10=87,67
