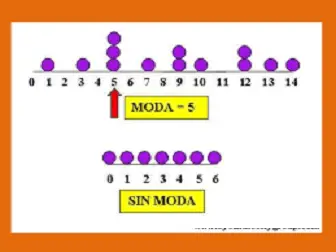
Los principales temas a analizar en medidas de tendencia central son la media, mediana, moda y rango, en el presente post hablaremos de la moda. El significado de la moda es el dato que más se repite. Te mostramos 3 interesantes ejemplos de moda para aprender. Puede haber más de una moda si existen varios datos que se repiten el mismo número de veces a lo que se denomina multimodal y puede que no exista moda si ningún dato se repite.
Ejercicio 1
Las notas obtenidas del examen de matemáticas es de 15 alumnos son las siguientes: 5,3,9,7,3,6, 7,5,8,7,5,4,7,6 y 8.
Determinar la moda de las notas de las notas de matematicas.
Lo primero que hacemos es ordenamos los datos de menor a mayor:
3,3,4,5,5,5,6,6,7,7,7,7,8,8,9
La moda tiene un valor de 7 ya que es el numero que más se repite en el ejercicio.
Ejemplo 2
La siguiente tabla proporciona la cantidad de gatos y de perros que tienen en sus casas un grupo de 10 amigos:
| Gatos | Perros |
| 3 | 0 |
| 0 | 1 |
| 0 | 2 |
| 1 | 1 |
| 1 | 0 |
| 0 | 0 |
| 3 | 3 |
| 1 | 2 |
| 6 | 0 |
| 0 | 2 |
Calcular la moda del número gatos y la moda del número de perros.
Si sumamos la cantidad de los gatos y de los perros existentes, tenemos el número de mascotas de cada amigo. De la misma también se puede determinar la moda.
Solucionando el ejercicio
Se puede establecer que la moda del número de gatos es 0
Se puede establecer que la moda del número de perros es 0.
Se puede establecer la moda del número de mascotas, para lo que tenemos que sumar los datos de las filas, obteniendo los datos 3, 1, 2, 2, 1, 0, 6, 3, 6, 2. La moda es de 2 del número de mascotas.
Ejemplos de moda 3
El profesor realizó el número de anotaciones de los goles que marcaron sus 50 alumnos:
| Goles | Alumnos |
| 0 | 2 |
| 1 | 4 |
| 2 | 6 |
| 3 | 5 |
| 4 | 8 |
| 5 | 10 |
| 6 | 5 |
| 7 | 3 |
| 8 | 4 |
| 9 | 1 |
| 10 | 2 |
Calcular la moda
El número de goles que más se repite no existe, por lo tanto no hay una moda. En el caso de los alumnos se repite el valor de 5, siendo la moda este valor.
