
Una vez que tenemos visto los ejemplos, indicaremos algunas propiedades y como sacar la varianza.
¿Cómo se verá afectada la varianza si a un grupo de puntuaciones se le suma un valor constante? En general, la varianza persiste constante bajo la adición de una constante c a todas las puntuaciones de un grupo como se manifiesta a continuación:

Se puede evidenciar fácilmente esta propiedad si le sumamos un valor constante a cada uno de los datos del ejemplo de la serie simple y calculamos la varianza, con esto logramos ver que el valor no cambia.
¿Qué ocurre con la varianza si cada puntuación se multiplica por una constante?
En general, la varianza será igual a c2s2 siempre que las puntuaciones del grupo se multipliquen por una constante como a continuidad se demuestra:
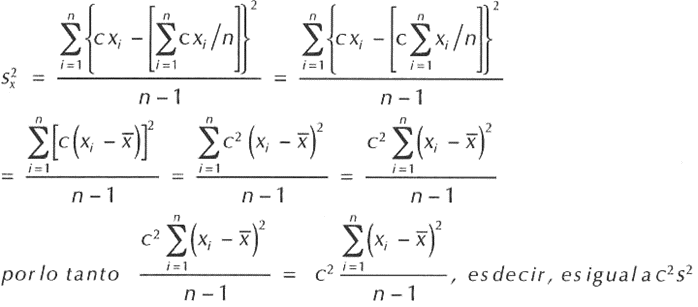
Ya que hemos visto la representación de calcular la varianza y algunas de sus propiedades en los desiguales tipos de series, es significativo mencionar que existe un segundo método para estimar la varianza, en el cual no se solicita calcular la media de la muestra y nunca es necesario lograr cada una de las desviaciones de la muestra.
Cabe explicar que esta fórmula se obtiene de la original ejecutando algunas manipulaciones algebraicas que veremos a continuación:
Partiendo de la fórmula original poseemos que:
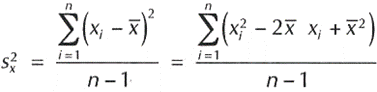
Como la sumatoria de una suma algebraica es igual a la suma algebraica de las sumatorias por lo tanto poseemos:
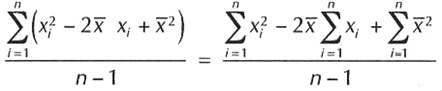
Poseyendo en cuenta que la expresión primero puede rescribirse de la subsiguiente forma:
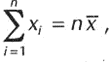
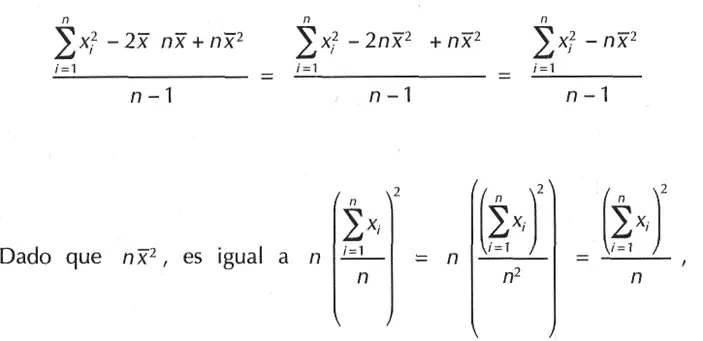
Entonces sustituyendo en la ecuación tenemos como sacar la varianza:
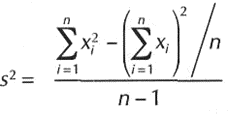
De esta forma se deduce la fórmula alternativa para calcular la varianza en la cual, como ya lo aludimos, no se tiene que calcular la media ni las desviaciones de los valores.
Como en el ejemplo de la primera fórmula, para las series de frecuencia y, de clases y frecuencias, la fórmula tiene que ser reformada en cada caso para que pueda ser aplicada. No manifestaremos las operaciones para llegar a cada resultado, únicamente mostraremos el resultado final como se muestra a continuación:

Ejemplos: arrebataremos los mismos datos que manejamos para calcular la varianza con el primer método y, así evidenciaremos que llegamos a los mismos resultados con este segundo método.
Para una serie simple como sacar la varianza
Calcular la varianza para los sucesivos valores:

Aplicando la fórmula:
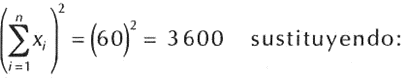
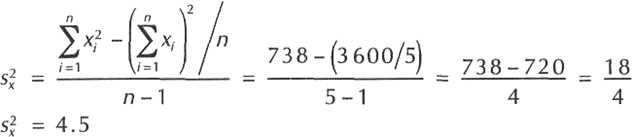
Como sacar la varianza para una serie de frecuencias
Considerando los siguientes valores, calcular la varianza:

Aplicando la fórmula:
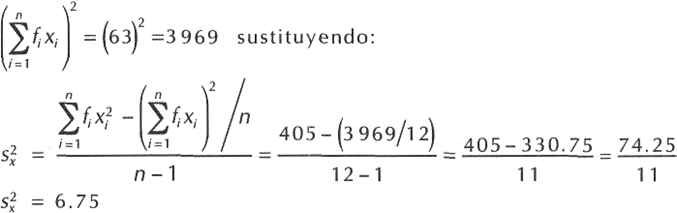
Para una serie de clases y frecuencias
Considerando los sucesivas datos calcular la varianza:

Aplicando la fórmula:
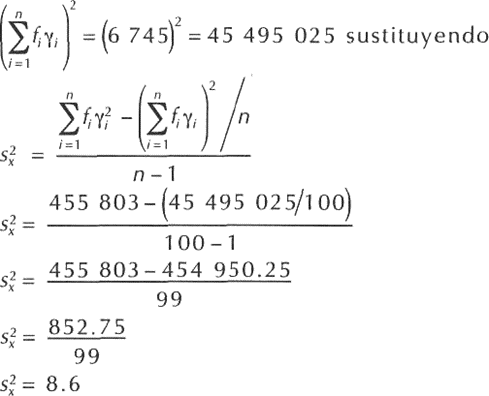
Finalmente, cabe indicar que el cálculo de la varianza tiene algún error cuando se trata del agrupamiento; de los datos en clases, designado error de agrupamiento; para ajustado a la contexto se utiliza la varianza corregida:
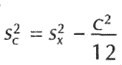
Donde c es el tamaño del intervalo de clase. La corrección se echar de ver como corrección de Sheppar, se maneja en distribuciones continuas donde los extremos van gradualmente a cero en uno y otro direcciones.
Los estadísticos difieren en lo que se refiere a cuándo y si debe aplicarse la corrección Sheppard. Positivamente no debe aplicarse sin tener hecho un examen completo de la situación, esto se debe a que impacientaba sobrecorregirse la muestra y así suplantar unos errores por otros.
