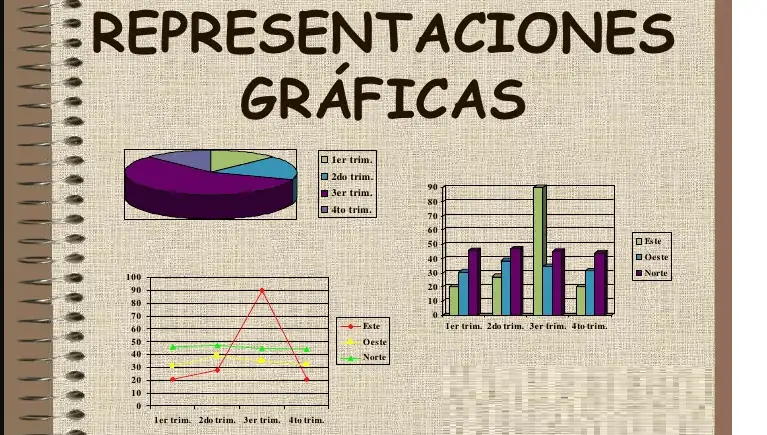
Constituye un instrumento de gran utilidad, las representaciones graficas estadistica de los datos ya que permite:
- Captar aspectos relevantes de la distribucion de frecuencias
- Mejorar la comprensión del fenómeno que se revisa
- Detectar la vida de errores en los datos.
Representaciones graficas estadistica: Diagrama de barras
En el eje de abscisas, para elaborar el gráfico se obtienen categorías o valores. Las frecuencias absolutas o relativas para el caso del eje de las ordenadas . Se alza una barra perpendicular al eje de abscisas encima la marca de cada categoría. La forma de estructurar es:
- Si se representan las frecuencias absolutas o relativas, la forma de estructurar el diagrama es el mismo.
- El criterio de orden de las categorías (datos cualitativos) más adecuado es el de mayor a menor frecuencia, en lo cual los valores (datos cuantitativos) van desde el menor al más enorme.
- Este gráfico permite visualizar rápidamente las categorías o valores más o menos comunes.
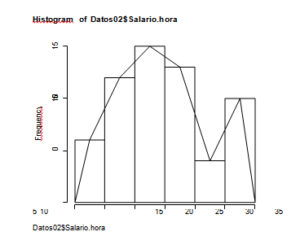
Representaciones graficas estadistica: Diagrama de Escalera
Se utiliza para representar las distribuciones de frecuencias absolutas o relativas acumuladas correspondientes a una variable discreta que toma pocos valores diferentes.
Para construir el diagrama se encuentran en el eje de abscisas los valores de la variable y en ordenadas las frecuencias acumuladas. Se marca coordenadas (xi,Ni) o (xi,Fi) según se represente frecuencias absolutas o relativas.
Desde todos esto se traza una recta paralela al eje de abscisas hasta el valor siguiente de X; hasta el punto (xi+1,Ni), debido a que entre dos valores consecutivos no hay acumulación de frecuencia. Los aspectos extremos de las líneas horizontales se incorporan con líneas verticales dando al diagrama el aspecto de escalera. Las características de este diagrama son:
- El más grande que alcanza el gráfico es n si se representan las frecuencias absolutas acumuladas o uno si se representan las frecuencias relativas acumuladas.
- La altura de los escalones es la frecuencia absoluta o relativa es xi.
- Para una variable X que toma solamente los valores x1, x2.
Histograma
En eje abscisas se pone los intervalos en los que se agrupa los valores de la variable. Encima del intervalo se dibuja un rectángulo cuya área debe ser en proporción a su frecuencia.
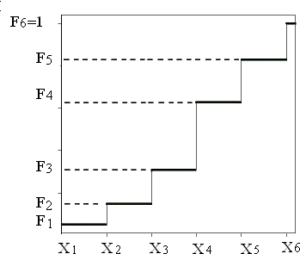
- Se dibujan los rectángulos con alturas iguales a las frecuencias, si todos los intervalos son de igual amplitud. En este ejemplo, el área de los diferentes rectángulos se vee proporcional a la frecuencia.
- Se debe calcular su densidad o altura de los rectángulos si la amplitud del intervalo es variable. Así, el sector de los rectángulos será igual a la frecuencia del intervalo. Densidad=Elevación= frecuencia/amplitud
En el histograma:
- Las áreas y no las alturas de los rectángulos son las que representan las frecuencias.
- Informa sobre la concentración existente de las diferentes observaciones en el intervalo, la altura de los rectángulos.
- El sector total es igual o proporcional al tamaño de la muestra.
- El sector total es igual o proporcional a 1, si se representan las frecuencias relativas.
- Depende del número elegido y la amplitud de los intervalos, el perfil del histograma.
- El perfil del histograma es el mismo tanto si se representa el reparto de frecuencias absolutas como la de frecuencias relativas.
Polígono de Frecuencias
Este gráfico permite resumir el perfil del histograma y la frecuencias se presentan encima a éste.
Señalando las marcas de clase en el lado superior de los rectángulos del histograma, se traza el polígono. Se ponen estos puntos de coordenadas (xi, ni) (marca de clase, frecuencia absoluta o relativa) con trazo constante y se cierra el polígono en sus extremos hasta cortar el eje de abscisas en los aspectos situados en las marcas de clase de dos hipotéticos intervalos trazados antes que el primero y empezando del último.
El polígono de frecuencias, muestra estas ventajas:
- Superponiéndolos, es más fácil comparar polígonos de varias distribuciones.
- La curva suavizada del polígono sugiere de forma más clara el posible modelo de probabilidad conveniente para describir el comportamiento de la población.
Polígono de Frecuencias acumuladas
El polígono de frecuencias acumuladas se utiliza para mostrar las distribuciones de frecuencias absolutas o relativas acumuladas correspondiente a una variable. La distribución en este caso se ha tabulado agrupando los valores en intervalos por ser de naturaleza continua o discreta que toma diversos valores diferentes.
El polígono se hace situando en el eje de abscisas las fronteras de los intervalos definidos en la tabla y en el de ordenadas las frecuencias acumuladas. Se señalan los aspectos correspondientes a los fronteras superiores y sus frecuencias acumuladas, (Li,Ni) o (Li,Fi) y con trazo constante se unen dichos puntos, empezando por el punto (L0,0) (límite inferior del intervalo uno, frecuencia acumulada cero) y acabando en el punto (Lk,n) o (Lk,1) (límite superior del último intervalo, frecuencia total acumulada).
Debido a que ya no se dispone de las observaciones correspondientes a cada intervalo, al hacer el gráfico se involucra que éstas se reparten uniformemente en el intervalo, por tal razon, la frecuencia se acumula de forma lineal.
Este tipo de gráfico es necesario realizarlo para:
- Localizar valores que acumulan una determinada frecuencia. Se fija la frecuencia acumulada en el eje vertical y está el precio correspondiente en el eje horizontal.
- Obtener el número o el porcentaje de observaciones con “menos que” o “más que” un precio determinado. Se pone en el eje vertical la frecuencia acumulada y el precio en el eje horizontal.
- Establecer el modelo de distribución poblacional asociado a la muestra analizada superponiendo los gráficos.
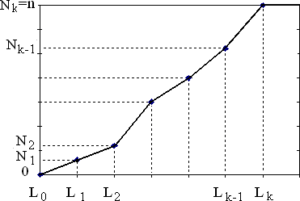
Diagrama de tallo y hojas
El diagrama de tallo y hojas es una técnica para exponer datos cuantitativos en formato gráfico.
Esta técnica da simultáneamente:
- La ordenación de los datos. Quedan ordenadas de menor a mayor todas las observaciones, lo que facilitará la localización de algunas medidas de síntesis como son la mediana y los cuantiles.
- La tabulación de los datos. Un intervalo cerrado define cada tallo por la izquierda y abierto por la derecha equivalente al intervalo de la tabla de frecuencias con valores agrupados.
- La representación gráfica del reparto. Es parecido al histograma que se obtendría de su correspondiente tabla de frecuencias el perfil del gráfico.
Al igual que el histograma, mediante el diagrama de tallo y hojas se visualizan diferentes puntos del reparto como son:
- Rango de los valores (dispersión)
- Localización de valores centrales
- Identificación de valores bastante o poco frecuentes
- Saltos (gaps) o lagunas
- Valores anómalos o extremos que están claramente desviados del conjunto de valores.
- Asimetría y forma.
Comparándolo con el histograma muestra las siguientes ventajas:
- No condensa la información.
- Se puede avanzar reconociendo los recursos de la muestra con una mínima pérdida de información.
- Posibilita la localización de los cuantiles.
- Informa de la vida de valores outliers y los identifica.
Para construir este diagrama:
- Se divide cada valor observado en hoja y tallo. Para ello, se fija la postura del dígito que se tomará como hoja (décimas, decenas, centenas) y los tallos quedan dados por los dígitos que quedan a la izquierda de la postura.
- Se anotan en columna los tallos desde el menor al mayor de manera sucesiva. Los tallos deben ser consecutivos y entender todo el recorrido de la variable.
- Se anotan de forma ordenada (de menor a mayor) sus hojas a la derecha del tallo.
- En el pie del gráfico se indica las unidades de la hoja para poder tener las observaciones en las unidades originales.
- Si el número de observaciones es grande, es conveniente que cada hoja represente a un número determinado de recursos con el mismo tallo y hoja, debiéndose indicar en el diagrama.
- Poniendolas a la izquierda de los tallos que se obtiene sumando las hojas correspondientes a cada tallo se puede concluir el diagrama con las frecuencias simples o acumuladas.
- Se indica el tamaño de la muestra, n, que es el número total de hojas en el encabezado.
- En la parte superior e inferior del diagrama se anotan los valores anómalos.
