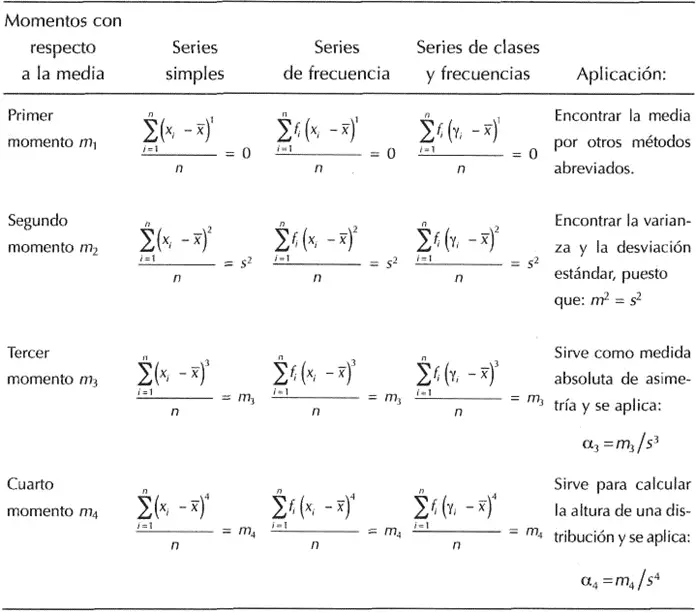
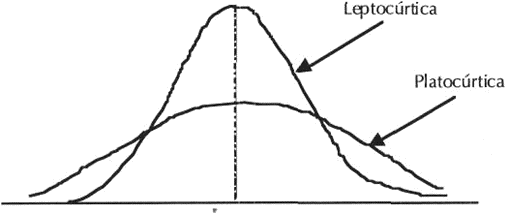
Dos distribuciones logran tener la misma media, la misma desviación estándar y ser afinadamente simétricas, pero siguen siendo diferentes si una es «puntiaguda» y la otra «achatada», a esto se llama medidas de curtosis. Las distribuciones puntiagudas y con extremos comparativamente anchos toman el nombre de leptocúrticas, en tanto que las que estiran a ser chatas y con colas relativamente estrechadas se citan platocúrticas. Estas distribuciones, gráficamente, tienen la sucesiva forma:
La forma formal para establecer la altura de una distribución es calculando el coeficiente de curtosis definido como a4 (alfa cuatro), que asimismo se precisa como el cuarto momento con relación a la media, definido por la siguiente fórmula para cada tipo de serie:

Donde: S4 = Elevar a la cuarta potencia la desviación estándar X – Media aritmética Y, = Valor de la marca de clase o punto medio de la clase
Esta medida de la altura no depende de la ubicación o varianza de la distribución y, por tanto, puede manejar con propósitos comparativos. La altura de la distribución «normal» es colocada comúnmente como el estándar de la altura que debe tener una distribución. Para una distribución normal, el valor del coeficiente de a4 = 3. Si en otras pruebas el valor del coeficiente de curtosis es mayor que 3, la distribución es leptocúrtica (en punta), mientras que si es mínimo que 3, es platocúrtica (achatada).
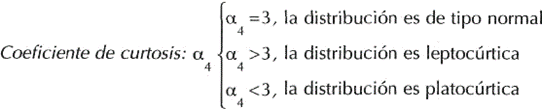
Advirtamos cómo se aplica el coeficiente de curtosis manejando el ejemplo anterior de las edades de 30 personas tomadas al azar.
a. Calcular las medidas de curtosis (coeficiente de curtosis) para la distribución.
Respuesta: si las edades de las treinta personas son las sucesivas:
| 3 0 | 3 2 | 2 1 | 3 7 | 2 6 | 4 3 | 1 8 | 3 7 | 2 3 | 3 5 |
| 2 7 | 4 4 | 3 9 | 3 9 | 4 0 | 4 0 | 2 8 | 3 9 | 4 2 | 4 0 |
| 39 | 42 | 37 | 40 | 35 | 37 | 39 | 25 | 39 | 22 |
Y si el valor de la media y la desviación estándar son:
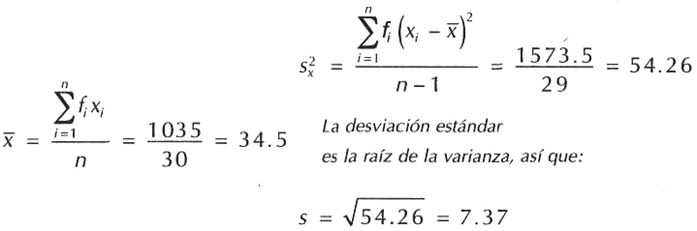
Entonces, empleando la fórmula conveniente para calcular el valor del coeficiente de curtosis, el valor que no tenemos calculado es la suma de las diferencias elevadas a la cuarta potencia, pero eso consecuencia muy fácil si reflexionamos que ya poseemos calculadas las diferencias al cuadrado, basta con elevar al cuadrado estas diferencias.
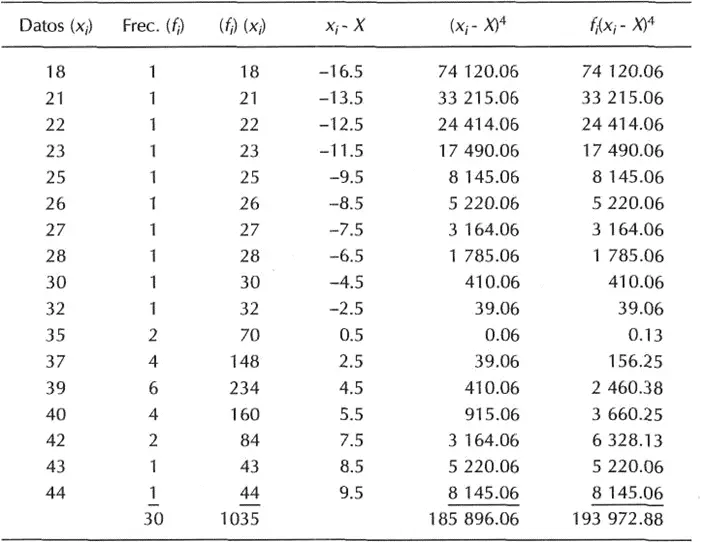
Para calcular las medidas de curtosis (el coeficiente de curtosis) de la distribución manejaremos la fórmula para una muestra ordenada en frecuencias:
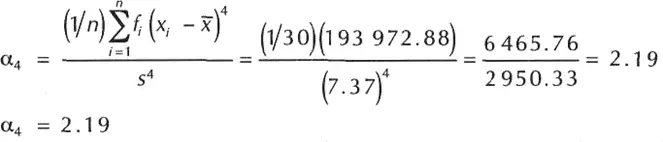
Podemos ultimar que como el valor del coeficiente de curtosis es mínimo que tres, entonces la distribución se puede reflexionar del tipo platocúrtica o achatada.
Finalmente, mostraremos un cuadro que resume los cuatro instantes con respecto a la media y lo que establece cada uno de ellos: