Medidas de asimetria

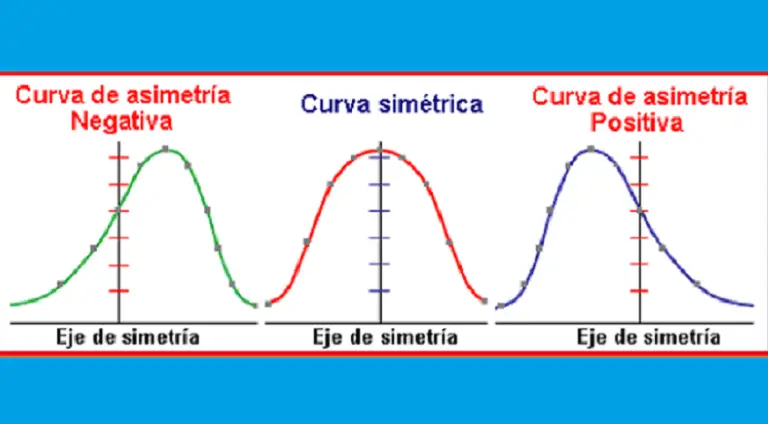
En secciones anteriores se han desarrollado métodos para describir la tendencia central de un conjunto de valores: media, mediana y la moda, y también para medir su grado de dispersión: varianza y desviación estándar. Otra característica que puede medirse de un conjunto de valores son las medidas de asimetria y de curtosis.

Conociendo esos resultados será posible resumir eficazmente las características de un conjunto de datos con cuatro indicadores: una medida de centralización (la media), una medida de dispersión (desviación estándar), una medida de asimetría y una medida de altura (curtosis). Veamos entonces como se calculan las medidas de asimetría y curtosis.

Representación grafica de Medidas de asimetria

Si la representación gráfica de un conjunto de valores es perfectamente simétrica, coincidirán los valores de la media, la mediana y la moda.

Una gráfica de este estilo quedaría de la siguiente forma:

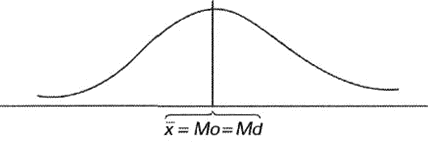
Conforme la distribución se aleja de la simetría los tres valores se alejarán entre sí, siendo la diferencia mayor la que se encuentra entre la media y la moda (véase gráficas a y b).

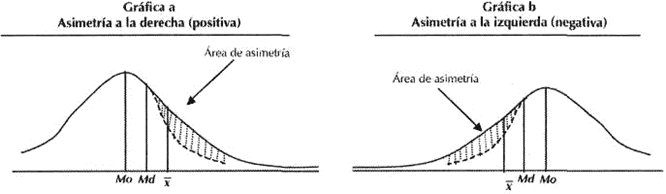
La asimetría es positiva o hacia la derecha, si la media es mayor a la mediana (gráfica a), y es negativa o hacia la izquierda si la mediana es mayor a la media (gráfica b).

La forma para calcular la asimetría que más se utiliza es el coeficiente de asimetría, definido como: a₃, que también se define como el tercer momento con respecto a la media y se encuentra definida por la siguiente fórmula para cada tipo de serie:

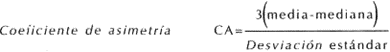
Donde:

Esta medida de la asimetría es un número relativo y, por lo tanto, puede utilizarse con fines de comparación.

Para calcular a₃, se obtiene primero la suma del cubo de las diferencias con respecto a la media. Luego se divide el resultado entre el número de observaciones y el resultado que se obtiene se divide entre el cubo de la desviación estándar.

Los posibles resultados se interpretan de la siguiente forma: para una distribución simétrica, a₃, es igual a cero. Los valores positivos de  a₃, indican que la asimetría de la distribución es positiva, en otras palabras, la distribución tiene un largo extremo (o cola), hacia la derecha. Los valores negativos de a₃, indican que la distribución tiene una larga cola hacia la izquierda. Entre mayor sea el valor de a₃, mayor será la asimetría de la muestra. Podemos resumir los posibles resultados en el siguiente diagrama:

Ahora veamos un ejemplo para ver cómo se obtiene el coeficiente de asimetría a partir de los siguientes datos de las edades de treinta personas elegidas al azar.

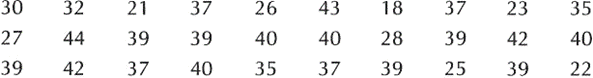
1. Resumir la información en un cuadro de frecuencias.
   1. Calcular la media y la desviación estándar.
   1. Obtener la asimetría de distribución.

Solución:

1. Resumir la información en un cuadro de frecuencias:

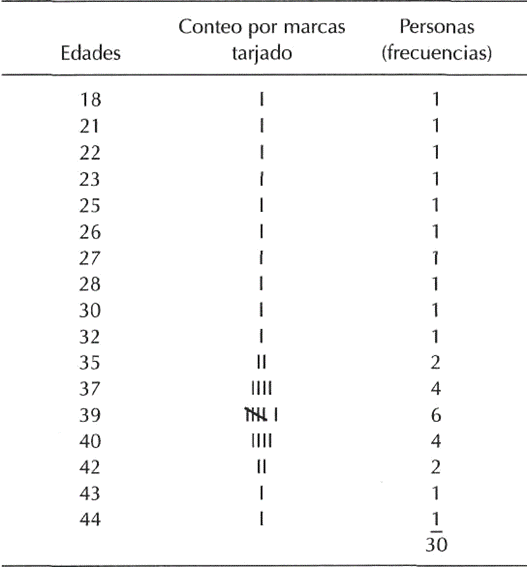
• Calcular la media y la desviación estándar:

Rara calcular la media y la desviación estándar es conveniente presentar la información en una tabla que nos permita realizar los cálculos con facilidad:

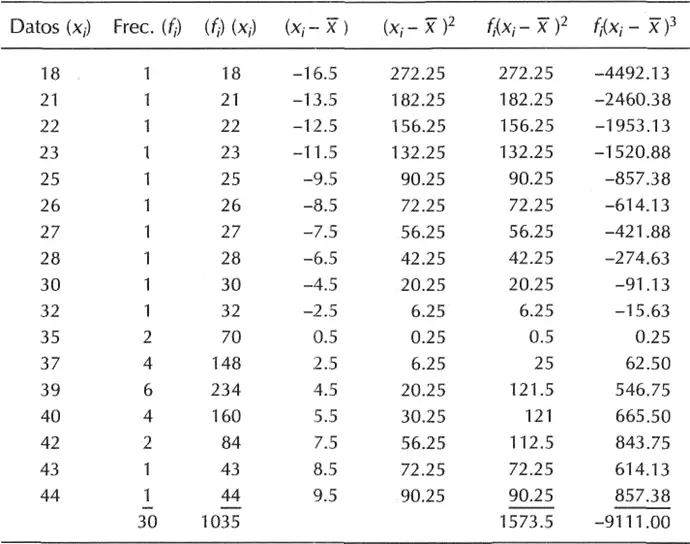
Una vez construida la tabla procedemos a calcular la media y la desviación estándar.

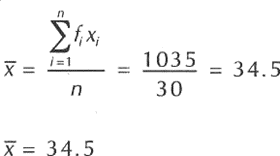
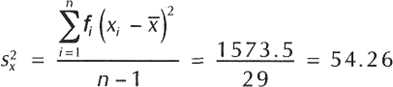
La desviación estándar es la raiz de la varianza, así que:

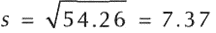
• c)    La asimetría de la distribución: Utilizamos la fórmula para el cálculo del coeficiente de asimetría en una muestra ordenada por frecuencias:

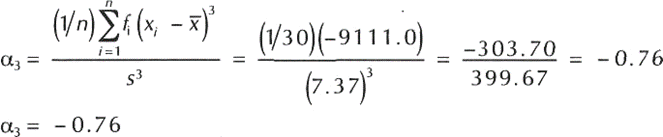
Podemos concluir que el valor de alfa tres es menor que cero y por lo tanto el coeficiente de asimetría nos indica que los datos presentan un sesgo negativo, es decir, presentan una larga cola hacia la izquierda. Esto lo podemos comprobar si graficamos los valores de las edades con respecto a sus frecuencias:

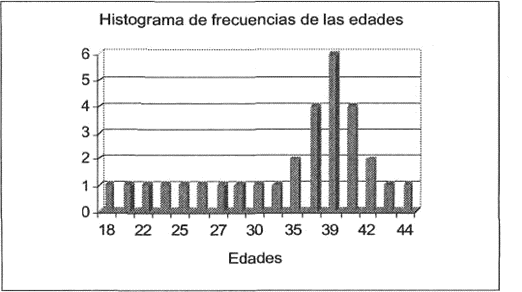
Como podemos observar en la gráfica, los datos de esta muestra sí presentan un sesgo negativo (es decir hacia la izquierda).