
Los datos recolectados tienen la posibilidad de corresponder a una población o muestra como se puede ver en este post que muestra ejemplos de datos estadisticos. En los dos casos los métodos de resumen de datos son análogos y designaremos por:
- Tamaño poblacional estudiada
- Tamaño de la muestra (parte de la población)
Con la intención de hacer un mejor análisis de los datos se necesita acomodar éstos, por medio de la utilización de distribuciones de frecuencia.
Una repartición de frecuencia es una tabla resumen en la que se disponen los datos divididos en equipos ordenados numéricamente que se llaman clases o categorías.
Ejemplos de datos estadisticos
La obra de una repartición de frecuencia de atributos o repartición de frecuencia de variable cualitativa es sencilla, basta enumerar los múltiples atributos con su respectiva frecuencia de ocurrencia.
Frecuencia absoluta: sugiere el número de veces que se repite un atributo.
A) Tabulación de variable discreta
Las tablas de frecuencia de variable discreta llevan 5 columnas donde los recursos que participan son los próximos:
a) Frecuencia absoluta: sugiere el número de veces que se repite una variable.
b) Tamaño de la muestra: sugiere la proporción de recursos que componen la muestra, se recibe sumando cada una de las frecuencias absolutas.
![]()
c) Frecuencia relativa: es la cantidad de datos que está en una clase, se recibe dividiendo la frecuencia absoluta de la clase por la magnitud de la muestra.
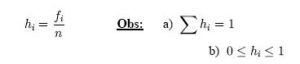
d) Frecuencia absoluta acumulada: sugiere la proporción de datos que se hallan hasta cierta clase.
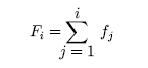
e) Frecuencia relativa acumulada: es la cantidad de datos acumulados que se hallan hasta cierta clase.

Ejercicios y ejemplos de datos estadisticos
Una compañía que tiene 50 trabajadores recomienda reestructurar las remuneraciones, se estudia los años de servicio de los trabajadores determinándose los próximos resultados:
| 4 | 5 | 4 | 6 | 7 | 9 | 7 | 7 | 5 | 8 |
| 8 | 7 | 6 | 7 | 7 | .4 | 6 | 8 | 8 | 9 |
| 6 | 8 | 9 | 5 | 6 | 5 | 4 | 7 | 9 | 6 |
| 7 | 6 | 5 | .4 | 4 | 4 | 6 | 8 | 8 | 7 |
| 8 | 9 | 5 | 5 | 4 | 6 | 7 | 9 | 5 | 4 |
N=50 (tamaño de la población)
Se exige:
- Tabular la información.
- ¿ Qué proporción de trabajadores tiene 8 años de servicio ?.
- ¿ Qué porcentaje de trabajadores tiene 6 años de servicio ?.
- Si esos trabajadores que tengan a lo menos 7 años de servicio reciben un incremento del 8% .¿ Qué porcentaje de los trabajadores recibió el aumento?.
- Si todos los trabajadores que tengan a lo más 5 años de servicio reciben una bonificación de $20000. ¿Qué proporción de trabajadores recibió esa bonificación?.
- Si la compañía dictamina otorgar una bonificación particular de $13.200 por todos los años de servicio.¿ Cuánto va a ser el dinero primordial para consumar esa bonificación?.
Solución ejemplos de datos estadisticos
| Años de servicio | fi | hi | Fi | /i |
| .4 | 9 | 18 | 9 | 18 |
| 5 | 8 | 16 | 17 | 34 |
| 6 | 9 | 18 | 26 | 52 |
| 7 | 10 | 20 | 36 | 72 |
| 8 | 8 | 16 | .44 | 88 |
| 9 | 6 | 12 | 50 | 00 |
| Total | 50 | 100 |
- 8 trabajadores poseen 8 años de servicio
- El 18% de los trabajadores tiene 6 años de servicio.
- El cuarenta y ocho por ciento de los trabajadores recibió el crecimiento de salario.
- 17 trabajadores han recibido la bonificación.
- $ 4.197.600 se requieren para la bonificación por año de servicio.
b) Tabulación de variable continua
Para tabular una variable continua se requieren:
a) Rango o recorrido: Es la diferencia entre el costo más alto y costo mínimo que toma la variable.
R= Xmax – Xmin
b) Número de intervalos o clases (m): Es el número de conjuntos en que es viable dividir los valores de la variable.
El número de clases no debería ser ni bastante enorme ni diminuto porque un número diminuto de clases puede ocultar la naturaleza general de los datos y un número enorme podría ser no descriptivo como para revelar alguna información eficaz. Como regla general se ofrece que el número de clases se encuentre entre 5 y veinte.

c) Amplitud del intervalo: Se refiere a la extensión o la amplitud del intervalo.
d) Parámetros de un intervalo: Son los valores extremos de una clase. El menor valor es considerado como el límite inferior y el que se recibe sumando al límite inferior a la amplitud del intervalo es el límite inferior de la segunda clase.
e) Parámetros reales de un intervalo: Se obtienen calculando el promedio entre el límite preeminente de una clase y el límite inferior de la clase siguiente.
f) Marca de clase: Es el punto medio de un intervalo.
g) Frecuencia absoluta: sugiere el número de visualizaciones que forma parte de un intervalo dado.
h) Frecuencia relativa: es la cantidad de datos que está en un intervalo, se establece dividiendo la frecuencia absoluta del intervalo por la magnitud de la muestra.
i) Frecuencia absoluta acumulada: sugiere el número de datos de la muestra menores o equivalentes al límite real preeminente del intervalo i.
