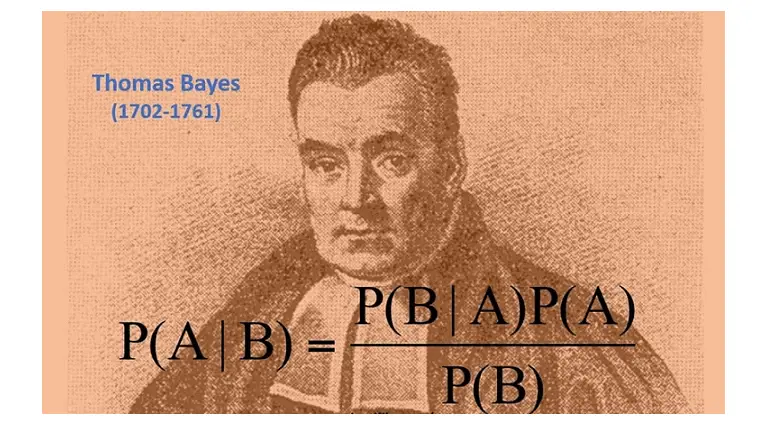
Thomas Bayes Nacio en Londres, Inglaterra en 1702 y fallecio en 1761 quien fue un matemático y ministro presbiteriano. Su obra más conocida el Teorema de Bayes.
El teorema que lleva su nombre tiene relación con la probabilidad de un evento condicionado por la ocurrencia de otro evento.
Thomas Bayes 1763
En la teoría de la probabilidad, el teorema de Bayes es una proposición planteada por el matemático inglés Thomas Bayes y publicada póstumamente en 1763 que expresa la probabilidad condicional de un acontecimiento aleatorio dado en términos del reparto de probabilidad condicional del acontecimiento dado y el reparto de probabilidad marginal.
En términos generales, el teorema de Bayes es de gran relevancia pues vincula la probabilidad de un hecho con la probabilidad de otro.
O sea, ejemplificando, que sabiendo la probabilidad de tener un dolor de cabeza ya que se tiene gripe, se podría saber, la probabilidad de tener gripe si se tiene un dolor de cabeza. Muestra este sencillo ejemplo la alta relevancia del teorema en cuestión para la ciencia en cada una de sus ramas, pues tiene vinculación íntima con la comprensión de la probabilidad de puntos causales dados los efectos vigilados.
En el caso de que exista un grupo de sucesos mutuamente excluyentes y exhaustivos tal que la probabilidad de todos ellos es diferente de cero. Si es un evento cualquier persona del que se conocen las probabilidades condicionales entonces la probabilidad es dada por:
donde:
- son las probabilidades a priori,
- es la probabilidad de conjetura,
- son las probabilidades después.
Regla de Bayes.
Basado en la definición de probabilidad condicionada se recibe la Fórmula de Bayes, además famosa como Regla de Bayes.
Esta fórmula nos posibilita calcular la posibilidad condicional de cualquier persona de los eventos dado. La fórmula ha originado especulaciones del tipo filosófico.
Es válido en cada una de las aplicaciones de la teoría de la probabilidad el teorema de Bayes. No obstante, existe una discusión sobre el tipo de probabilidades que emplea. Los seguidores de la estadística clásica solo aceptan probabilidades fundamentadas en experimentos repetibles y que tengan una aseveración experimental mientras tanto que los denominados estadísticos bayesianos permiten probabilidades subjetivas. El teorema puede servir entonces para indicar cómo debemos cambiar nuestras propias probabilidades subjetivas una vez que hemos recibido información adicional de un experimento.
La estadística bayesiana está mostrando su utilidad en ciertas estimaciones fundamentadas en el razonamiento personal a priori y el producido de permitir verificar aquellas estimaciones en funcionalidad de la prueba experimental es lo cual está abriendo novedosas maneras de hacer entendimiento. Los clasificadores bayesianos son una aplicación de esto que son muchas veces utilizados en implementaciones de filtros que se adaptan con la utilización. Otra tipo de aplicación está en la fusión de datos, combinando información expresada en términos de densidad de probabilidad perteneciente de diversos sensores.
Como observación, se recibe la siguiente fórmula y su demostración resulta trivial.
Como aplicaciones puntuales:
- El diagnóstico de cáncer.
- A lo largo del juego de poker se evaluan las probabilidades.
- Probabilidades a priori y después.
- Ley de sucesión de Laplace.
- En el testeo de conjetura en Ciencia Política.
Probabilidad inversa
Se resuelve el problema conocido como «probabilidad inversa» con su teorema. En otras palabras, apreciar probabilísticamente las probables condiciones que rigen supuesto que se ha visto cierto evento. Hablamos de posibilidad «inversa» en el sentido de que la «directa» podría ser la posibilidad de mirar algo supuesto que rigen ciertas condiciones.
Los que siguen la inferencia bayesiana aseguran que la trascendencia de la probabilidad inversa se basa en que es ella la que realmente atrae a la ciencia, ya que procura sacar conclusiones en general desde lo objetivamente visto, y no al revés.
Bayes ha sido uno de los primeros en usar la posibilidad inductivamente y implantar una base matemática para la inferencia probabilística.
Thomas Bayes 1969
En reconocimiento al fundamental trabajo que hizo Thomas Bayes en temas de probabilidades, su tumba ha sido restaurada en 1969 con donativos hechos por estadísticos de todo el planeta.
En la actualidad, basado en su obra, se ha desarrollado una poderosa teoría que ha conseguido notables aplicaciones en las más distintas zonas del entendimiento. Particular connotación tuvieron los sistemas para detección de spam en el ambiente de Internet. El enfoque de la inferencia bayesiana en el campo sanitario, experimenta un desarrollo sostenido, en especial en lo cual concierne al estudio de ensayos clínicos, donde comentado enfoque vino interesando de forma creciente a las agencias reguladoras de los medicamentos, como por ejemplo la norteamericana.
