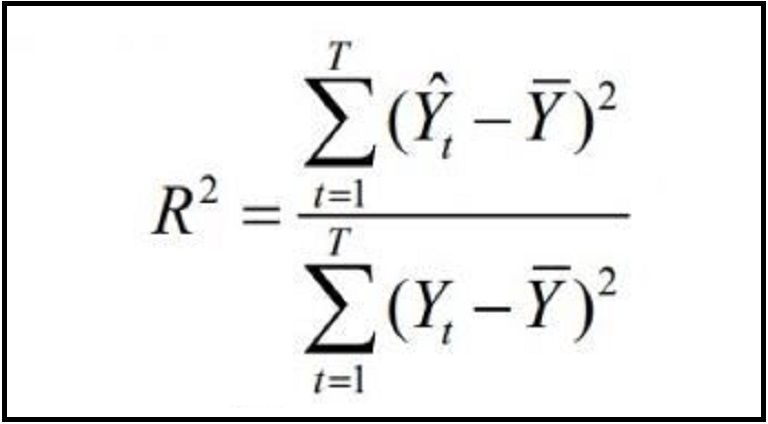
El R 2 es una medida estadística de qué tan junto están los datos de la línea de regresión justa. También se llama como coeficiente de determinación, o coeficiente de valor múltiple si se trata de regresión múltiple.
La enunciación de R 2 es bastante sencilla: es el % de la variación en la variable de respuesta que es expuesto por un modelo lineal. Es decir:
R-cuadrado = Variación explicada / variación total
El R-cuadrado está entre 0 y 100%:
- 0% muestra que el modelo no explica ninguna porción de la variabilidad de los datos de respuesta en torno a su media.
- 100% muestra que el modelo expone toda la variabilidad de los datos de respuesta en torno a su media.
En ordinario, cuanto mayor es el R-cuadrado, excelente se ajusta el modelo a los datos. Pero, hay condiciones significativos con respecto a esta pautante.
Representación gráfica del r 2
Representar gráficamente los valores ajustados en destino de los valores observados ilustra desiguales valores del R-cuadrado en modelos de regresión.
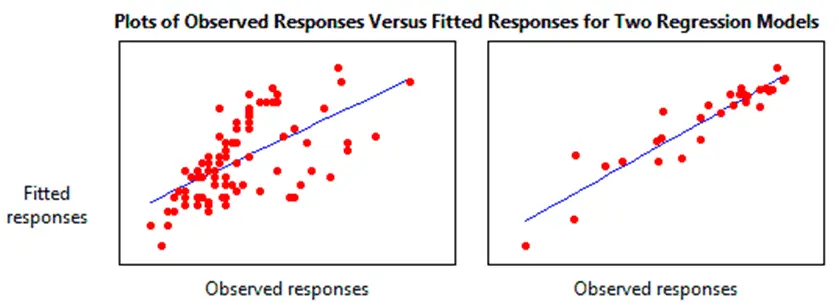
El modelo de regresión de la izquierda expone el 38% de la varianza y de la derecha revela el 87,4%. Cuanto mayor sea la varianza expuesta por el modelo de regresión, más cerca quedarán los puntos de los datos de la línea de regresión ajustada.
En suposición, si un modelo pudiera explicar el 100% de la varianza, los valores ajustados eternamente existirían iguales a los valores observados y por tanto los puntos de los datos existirían sobre la línea de regresión ajustada.
Limitaciones claves del r 2
El R-cuadrado no puede establecer si las estimaciones y predicciones de los coeficientes están sesgadas, y es por eso que se corresponden examinar las gráficas de residuos.
El R-cuadrado no muestra si un modelo de regresión es conveniente. Se logra tener un valor bajo del R-cuadrado para un modelo conveniente o un valor alto del R-cuadrado para un modelo que no se ajusta a los datos.
¿Son inherentemente malos los valores bajos del r-cuadrado?
Existe 2 razones primordiales por las que los valores bajos del R-cuadrado podrían pensarse correctas.
En unos campos, se aguarda que los valores del R-cuadrado sean bajos. Por ejemplo, cualquier disciplina que pretende predecir la conducta humano, como la psicología, regularmente tiene valores del R-cuadrado menor al 50%. Los seres humanos son absolutamente más difíciles de anunciar que, por ejemplo, los procesos físicos.
Asimismo, si el valor del R-cuadrado es bajo pero se tiene predictores estadísticamente reveladores, aún se puede lograr conclusiones significativas acerca de la asociación entre los cambios en los valores de los predictores y los cambios en el valor de respuesta. Soberanamente del R-cuadrado, los coeficientes significativos aún simbolizan el cambio medio en la respuesta para una unidad de cambio en el predictor mientras se conservan constantes los otros predictores del modelo.
