
La ciencia de datos suministra una gran cantidad de algoritmos de clasificación entre los que esta el random forest. Existen otros algoritmos de clasificación como la regresión logistica, la máquina de vectores de soporte, el clasificador de Bayes ingenuo y los árboles de decisión.
En esta publicación, inspeccionaremos cómo marchan los árboles de decisión básicos, cómo se conciertan los árboles de decisión individuales para establecer un random forest y, en última instancia, descubriremos por qué los random forest son tan buenos en lo que hacen.
Árboles de decisión
Repasemos velozmente los árboles de decisión, ya que son los mecanismos básicos del modelo de random forest. Favorablemente, son bastante intuitivos. Estaría dispuesto a apostar que la mayoría de las personas han usado un árbol de decisiones, a sabiendas o no, en algún instante de sus vidas.
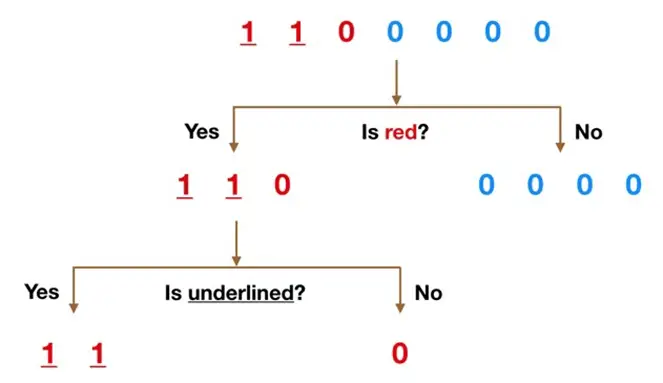
Ejemplo de árbol de decisión simple
Posiblemente sea mucho más fácil pensar cómo funciona un árbol de decisión a través de un ejemplo.
Conjeture que nuestro conjunto de datos consta de los números en la parte superior de la figura a la izquierda. Poseemos dos 1 y cinco 0 y queremos separar las clases usando sus características. Los tipos son el color (rojo frente a azul) y si la observación está subrayada o no.
El color juzga una característica suficiente obvia para dividir, ya que todos menos uno de los 0 son azules. Entonces logramos usar la pregunta, «¿Es rojo?» para dividir nuestro primer nodo. Logra pensar en un nodo en un árbol como el punto donde la ruta se divide en dos: las observaciones que efectúan los criterios descienden por la rama Sí y las que no descienden por la rama No.
La rama No es todo 0 ahora, así que hemos acabado allí, pero nuestra rama Sí aún se puede dividir aún más. Ahora logramos usar la segunda función y preguntar: «¿Está subrayado?» para hacer una segunda división.
Los dos 1 que viven subrayados descienden por la subrama Sí y el 0 que no está subrayado baja por la subrama derecha y hemos acabado. Nuestro árbol de decisiones pudo usar las dos características para dividir los datos cabalmente.
Comprensiblemente, en la vida real, nuestros datos no serán tan limpios, pero la lógica que emplea un árbol de decisiones sigue siendo la misma. En cada nodo, preguntará:
¿Qué característica me admitirá dividir las observaciones disponibles de modo que los grupos resultantes sean lo más diferentes posible entre sí ?
El clasificador de random forest
Random forest, como su nombre lo muestra, consiste en una gran cantidad de árboles de decisión individuales que maniobran como un conjunto. Cada árbol individual en el random forest escupe una predicción de clase y la clase con más votos se transforma en la predicción de nuestro modelo.
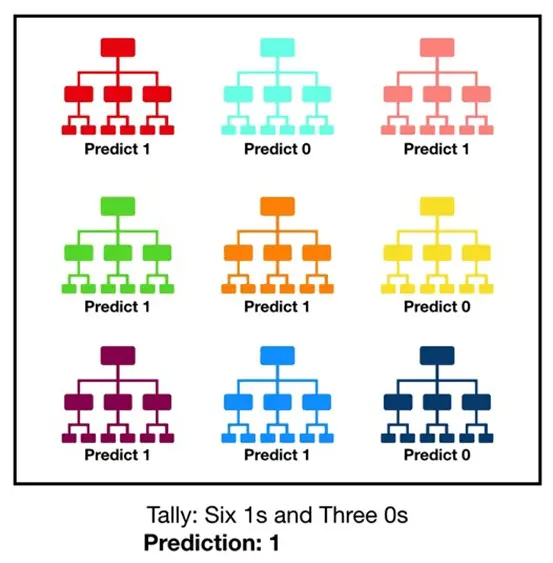
Visualización de un modelo de random forest
El concepto primordial detrás del random forest es simple pero eficaz: la sabiduría de las multitudes. En cláusulas de ciencia de datos, la razón por la que el modelo de random forest funciona tan bien es:
Una gran cantidad de modelos relativamente no correlacionados que marchan como un comité prevalecerán a cualquiera de los modelos constituyentes individuales.
La baja correlación entre modelos es la clave. Al igual que las inversiones con correlaciones bajas se unen para constituir una cartera que es mayor que la suma de sus partes, los modelos no correlacionados logran producir predicciones en conjunto que son más precisas que cualquiera de las predicciones individuales.
La razón de esta maravilloso consecuencia es que los árboles se resguardan entre sí de sus errores individuales (siempre y cuando no se equivoquen firmemente en la misma dirección). Si bien cualesquiera árboles pueden estar equivocados, muchos otros árboles vivirán en lo correcto, por lo que, como grupo, los árboles pueden moverse en la dirección correcta. Entonces, los requisitos previos para que el bosque aleatorio funcione bien son:
- Es preciso que haya alguna señal real en nuestras funciones para que los modelos creados con esas funciones marchen mejor que las conjeturas aleatorias.
- Las predicciones (y por lo tanto los errores) ejecutadas por los árboles individuales deben tener bajas correlaciones entre sí.
Un ejemplo de por qué los resultados no correlacionados son tan buenos
Los maravillosos efectos de tener muchos modelos no correlacionados es un concepto tan crítico que quiero exponer un ejemplo para ayudarlos a alcanzar realmente. Imaginen que estamos jugando el siguiente juego:
- Utilizo un generador de números aleatorios uniformemente distribuidos para ocasionar un número.
- Si el número que género es mayor o igual a 40, ganas (60% de sucesos de victoria) y te pago algo de dinero. Si existe por debajo de 40, gano y me pagas la misma cantidad.
- Ahora te ofrezco las consecutivas opciones.
- Juego 1: juega 200 veces, apostando $1 cada vez.
- Juego 2: juega 20 veces, apostando $10 cada vez.
- Juego 3: juegue dos veces, apostando $100.
¿Cuál elegirías? El valor esperado de cada juego es el mismo:
Juego de valor esperado 1 = (0,60*1 + 0,40*-1)*200 = 40
Valor esperado Juego 2= (0.60*10 + 0.40*-10)*20 = 40
Valor esperado Juego 3= (0,60*100 + 0,40*-100)*2 = 20
